Logistic Regression model은 여러 개의 binary classifier를 이용하여 multiple 클래스를 구현할 수 있다.
이를 Softmax Regression 혹은 multinomial logistic regression이라 표현 가능
개념
샘플 x가 주어지면
softmax regression model이 각 클래스 k에 대한 점수를 계산하고,그 점수에 softmax function을 적용하여 각 클래스의 확률을 추정.

위 s는 x가 주어졌을 때 각 클래스 k에 대한 점수다.
--
$$\textcolor{red}{\text{각 클래스는 자신만의 파라미터 벡터} θ^{(k)} \text{가 존재}} $$
--
이 벡터들은 파라미터 행렬(parameter matrix) Θ에 저장된다.
(1) 샘플 x에 대해 각 클래스의 점수가 계산되면
(2) softmax 함수를 통과시켜 클래스 k에 속할 확률(p)를 추정할 수 있다.
이 함수는 간단히 보면 각 점수에 지수 함수를 적용한 후 정규화를 한다.
(모든 지수 함수 결과의 합으로 나눔)

이 글의 내용은 많은 부분 아래 링크인 핸즈온 머신러닝 2판을 참고했으며
영리 목적이 아닌 개인적인 학습을 위해 정리한 내용을 바탕으로 작성했음을 밝힙니다.
K : 클래스 수
s(x) : 샘플 x에 대한 각 클래스의 점수를 담은 vector
$$σ(s(x))_{k} \text{: 샘플 x에 대한 각 클래스의 점수가 주어졌을 때 이 샘플이 클래스 k에 속할 확률}$$
logistic regression classifier와 마찬가지로 softmax regression classifier는 아래의 식처럼
추정 확률이 가장 높은 클래스(가장 큰 값을 가진 클래스)를 선택한다.
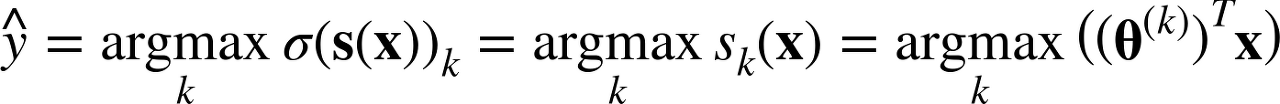
(argmax는 함수를 최대화하는 변수의 값을 반환)
softmax regression classifier는 한 번에 하나의 클래스만 예측한다.
즉, multi-class지 multi-output은 아니다.
따라서 종류가 다른 iris data와 같이 상호 배타적인 클래스에서만 사용해야 함.
하나의 사진에서 여러 사람의 얼굴을 인식하는데는 사용할 수 없음
softmax regression model 학습
학습의 목적
모델이 타겟 클래스에 대해서는 높은 확률을 가지고
타겟이 아닌 클래스에 대해서는 낮은 확률을 가지도록
하는 것이 궁극의 목표일 것이다.
아래는 cross entropy cost function이다

cross entropy cost function은
타겟 클래스에 대해 낮은 확률을 예측하는 모델을 억제하도록한다.
$$\text{위 식에서} y_{k}^{i} \text{는 i번째 샘플이 클래스 k에 속할 타겟 확률 - 일반적으로 샘플이 클래스에 속하는지 아닌지에 따라 1또는 0}$$
딱 두 개의 클래스만 있다면, 아래의 logistic regression의 cost function과 동일하다.
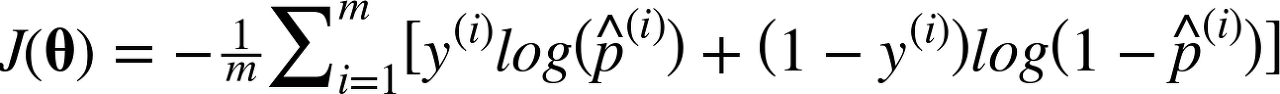
정리 중.,..
내용 참고
https://book.naver.com/bookdb/book_detail.nhn?bid=16328592
핸즈온 머신러닝
머신러닝 전문가로 이끄는 최고의 실전 지침서 텐서플로 2.0을 반영한 풀컬러 개정판 『핸즈온 머신러닝』은 지능형 시스템을 구축하려면 반드시 알아야 할 머신러닝, 딥러닝 분야 핵심 개념과
book.naver.com
'딥러닝관련 > 기초 이론' 카테고리의 다른 글
| ROC curve and AUC (0) | 2022.08.06 |
|---|---|
| Cross entropy loss 정리 (0) | 2022.03.06 |
| 로지스틱 회귀(logistic regression) (0) | 2022.03.02 |
| 규제가 있는 선형 모델 (0) | 2022.02.27 |
| 편향/분산 트레이드 오프 (Bias/variance trade-off) (0) | 2022.02.27 |



