Logistic regression
(or logit regression)
분류에서 사용할 수 있는 회귀 알고리즘
샘플이 특정 클래스에 속할 확률 추정하는데 널리 사용.(ex, 스팸일 확률? -> 50% 넘으면 스팸으로 분류)
추정 확률이 일정 기준치를 넘어가면 양성 클래스 (positive class)추정 확률이 일정 기준치를 넘지 못하면 음성 클래스 (negative class)
-> 이진 분류 (binary classification)
확률 추정
우선, linear regression 모델과 같이 logistic regression model은
입력 특성의 weight의 합을 계산(+ bias)
대신,
linear regression처럼 결과를 바로 출력하지 않고,
결과의 값의 logistic을 출력

σ(·)로 표현하는 logistic은 0과 1 사이의 값을 출력하는 sigmoid function


logistic regression model이 샘플 x가 양성 클래스에 속할 확률을 계산하면 이에 대한 예측 값을 쉽게 구할 수 있다.

sigmoid function에 근거하여
t < 0 이면 σ(t) < 0.5 이고
t ≥ 0 이면 σ(t) ≥ 0.5 이므로
logistic regression model은
model의 결과값(t : logit)이
양수일 때 1 (positive class)라고 예측하고
음수일 때 0 (negative class)라고 예측한다.
Training과 cost function
Training의 목적
positive sample(y=1)에 대해서는 높은 확률을 추정하고
negative sample(y=0)에 대해서는 낮은 확률을 추정하는
모델 파라미터 벡터 θ를 찾는 것
아래를 cost function으로 사용한다.
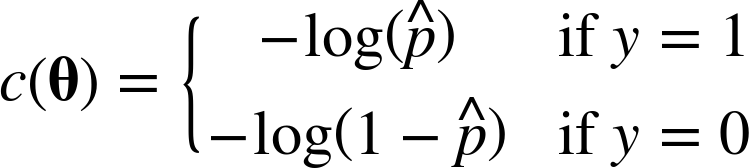
위 부분을 이해해보자..
positive sample(y=1)의 경우
만약 양성 샘플이면 -log(p)의 cost function이 적용될 것이다.
직관적으로 이해하도록 아래의 -log(p)의 그래프를 한 번 봐보자
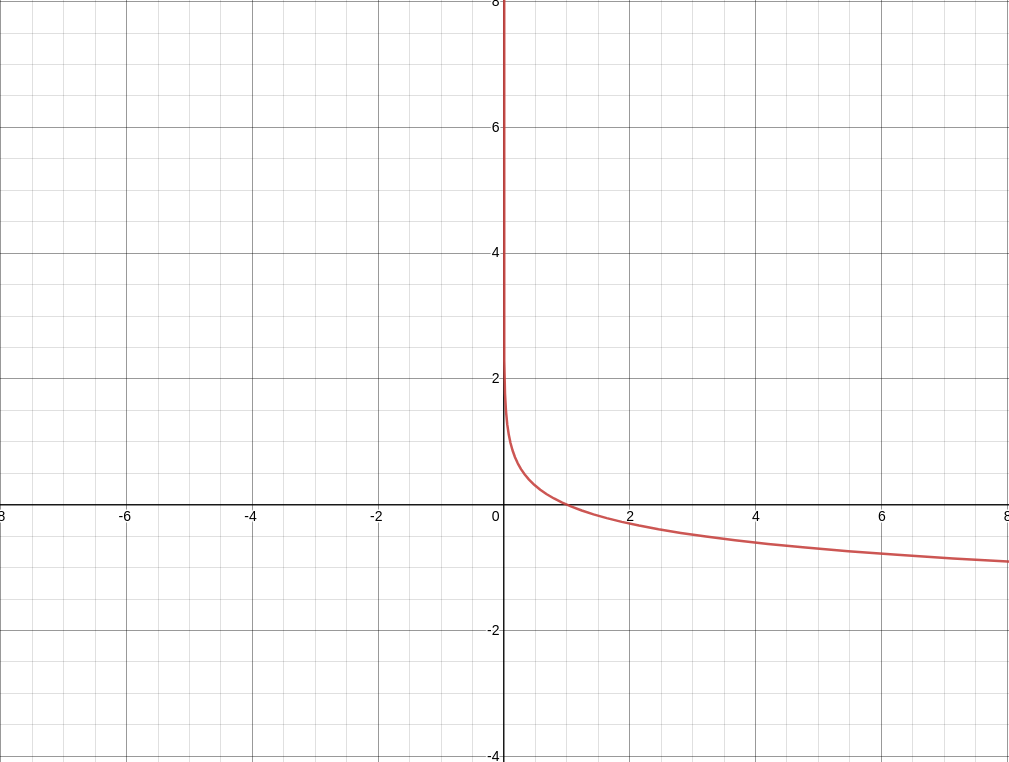
우리는 p가 0.5이상일 때 positive sample로 분류하기로 위에서 결정하였고
위에서 cost function을 정의한 거와 같이 y=1 즉, positive sample일 때,
위와 같은 -log(p) 그래프를 cost function으로 정의하였다.
정의된 cost function에 positive sample을 대입해보자.
만약 positive sample이고,
probability(p)가 높으면 -log(p)의 값이 작을 것이고
probability(p)가 낮으면 -log(p)의 값이 클 것이다.
이를 해석하자면,
--
positive sample의 p값이 커지면 커질수록, loss의 값은 줄어들고
positive sample의 p값이 작으면 작을수록, loss의 값은 늘어난다
--
는 의미다.
negative sample(y=0)의 경우
만약 음성 샘플이면 -log(1-p)의 cost function이 적용될 것이다.
동일한 방식으로 아래의 -log(1-p)의 그래프를 한 번 봐보자
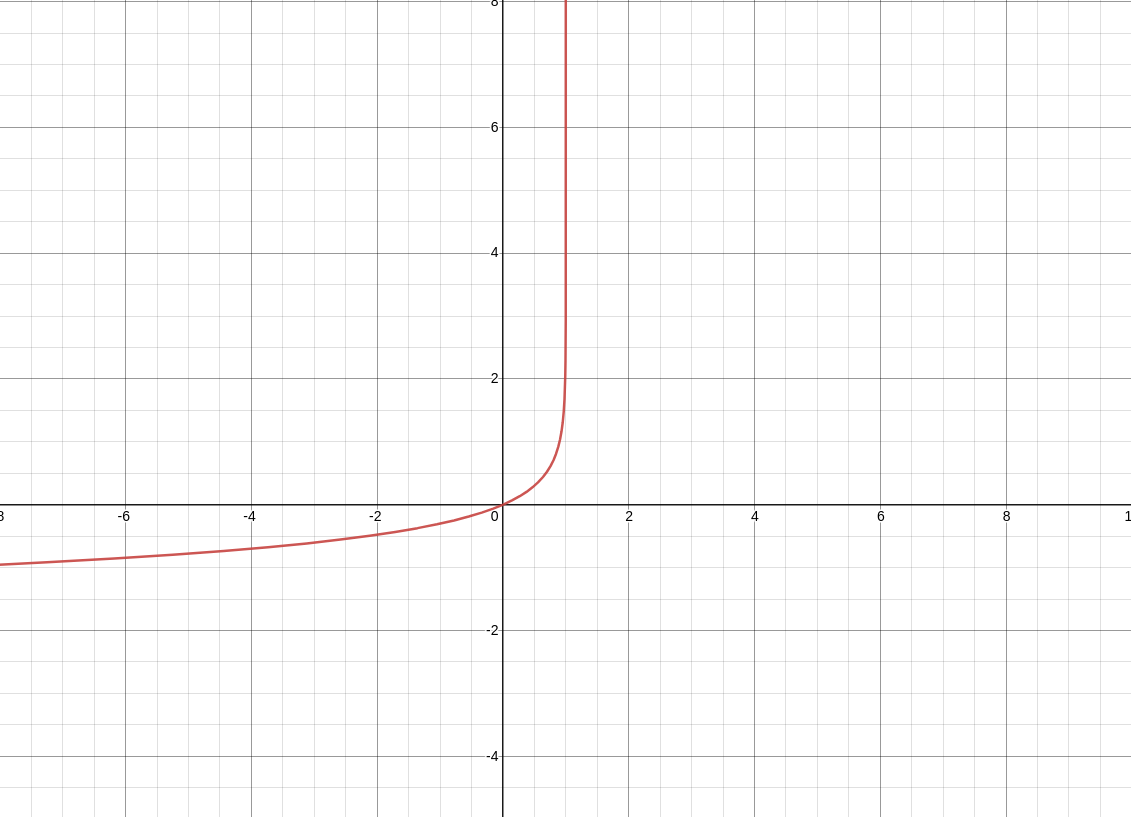
우리는 p가 0.5이하일 때 negative sample로 분류하기로 위에서 결정하였고
위에서 cost function을 정의한 것와 같이 y=0 즉, negative sample일 때,
위와 같은 -log(1-p) 그래프를 cost function으로 정의하였다.
정의된 cost function에 negative sample을 대입해보자.
만약 negative sample이고,
probability(p)가 높으면 -log(1-p)의 값이 클 것이고
probability(p)가 낮으면 -log(1-p)의 값이 작을 것이다.
이를 해석하자면,
--
negative sample의 p값이 커지면 커질수록, loss의 값은 늘어나고
negative sample의 p값이 작으면 작을수록, loss의 값은 줄어든다
--
는 의미다.
이를 요약하자면,
positive sample일 때, p의 값이 큰 것이 좋고,
negative sample일 때, p의 값이 작은 것이 좋다.
(cost를 적게 가져가기 때문)
cost function에 근거하여,
전체 training set에 대한 cost function은 모든 training sample의 cost를 평균한 것.
이를 log loss라고 불리며 아래와 같이 표기가 가능하다.

위 식을 잘 보면
positive class(y=1)의 경우 log(p)만 남게되고
negative class(y=0)의 경우 log(1-p)만 남게된다.
(이런 식을 연구한 사람들은 진짜 천재들 같다....)
위 cost function의 최솟값을 계산하는 알려진 해가 없다고 한다.
그러나 이 cost function은 convex(볼록)하기 때문에,
gradient descent 방법이 global minimum을 찾는 것을 보장한다
(learning rate가 크지 않고, 시간이 충분히 있다면).

위는 cost function의 j번째 파라미터 θj 에 대해 편미분을 한 것
잘 보면....
각 입력 샘플에 대해서 오차를 계산하고 j번째 입력 특성을 곱해서
모든 training sample에 대해 평균을 낸다.
모든 편도함수를 포함한 gradient vector를 만들면 gradient descent algorithm을 적용할 수 있다.
결정 경계(Decision Boundaries)
iris dataset을 이용하여 logistic regression을 해보자
from sklearn import datasets
iris = datasets.load_iris()
list(iris.keys())X = iris["data"][:, 3:] # 꽃잎 너비
y = (iris["target"] == 2).astype(int) # Iris virginica이면 1 아니면 0from sklearn.linear_model import LogisticRegressionlog_reg = LogisticRegression()
log_reg.fit(X, y)import numpy as np
import matplotlib.pyplot as plt
X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_proba[:, 1] >= 0.5][0]
plt.figure(figsize=(8, 3))
plt.plot(X[y==0], y[y==0], "bs")
plt.plot(X[y==1], y[y==1], "g^")
plt.plot([decision_boundary, decision_boundary], [-1, 2], "k:", linewidth=2)
plt.plot(X_new, y_proba[:, 1], "g-", linewidth=2, label="Iris virginica")
plt.plot(X_new, y_proba[:, 0], "b--", linewidth=2, label="Not Iris virginica")
plt.text(decision_boundary+0.02, 0.15, "Decision boundary", fontsize=14, color="k", ha="center")
plt.arrow(decision_boundary[0], 0.08, -0.3, 0, head_width=0.05, head_length=0.1, fc='b', ec='b')
plt.arrow(decision_boundary[0], 0.92, 0.3, 0, head_width=0.05, head_length=0.1, fc='g', ec='g')
plt.xlabel("Petal width (cm)", fontsize=14)
plt.ylabel("Probability", fontsize=14)
plt.legend(loc="center left", fontsize=14)
plt.axis([0, 3, -0.02, 1.02])
plt.show()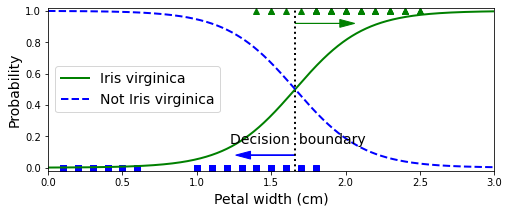
위 결과를 봐보자
Iris-Verginica(삼각형)의 꽃잎 너비는 1.4~2.5cm에 분포하고,
다른 데이터들은 0.1~1.8cm에 분포한다.
따라서 어쩔 수 없이 중첩되는 부분이 발생한다.
삼각형 부분을 다시 보자.
대략 petal width가 2cm를 넘어가면 높은 확률로 iris virginica로 예측하는 것을 알 수 있다.
(강한 ris virginica 확신)
반면, petal width가 1cm 아래면 높은 확률로 iris virginica가 아니라고 예측하는 것을 알 수 있다.
(강한 non iris virginica 확신)
이 두 극단 사이에는 분류가 확실하지 않다.
만약 클래스를 예측하려고하면 가장 가능성이 높은 클래스를 반환할 것임.
그렇기 때문에 양쪽(iris & non-iris)의 probability가
똑같이 50%가 되는 1.6cm 근방에서 decision boundary가 만들어진다.
이 경우 꽃입 너비가 1.6cm보다 크면 classifier는 iris-verginica로 예측하고
그보다 작으면 non iris-verginica로 예측할 것이다.
decision_boundary
# array([1.66066066])log_reg.predict([[1.7], [1.5]]) # 너비가 1.7cm 일때 / 1.5cm 일때 분류
# array([1, 0])
from sklearn.linear_model import LogisticRegression
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(int)
log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42)
log_reg.fit(X, y)
x0, x1 = np.meshgrid(
np.linspace(2.9, 7, 500).reshape(-1, 1),
np.linspace(0.8, 2.7, 200).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_proba = log_reg.predict_proba(X_new)
plt.figure(figsize=(10, 4))
plt.plot(X[y==0, 0], X[y==0, 1], "bs")
plt.plot(X[y==1, 0], X[y==1, 1], "g^")
zz = y_proba[:, 1].reshape(x0.shape)
contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg)
left_right = np.array([2.9, 7])
boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1]
plt.clabel(contour, inline=1, fontsize=12)
plt.plot(left_right, boundary, "k--", linewidth=3)
plt.text(3.5, 1.5, "Not Iris virginica", fontsize=14, color="b", ha="center")
plt.text(6.5, 2.3, "Iris virginica", fontsize=14, color="g", ha="center")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.axis([2.9, 7, 0.8, 2.7])
plt.show()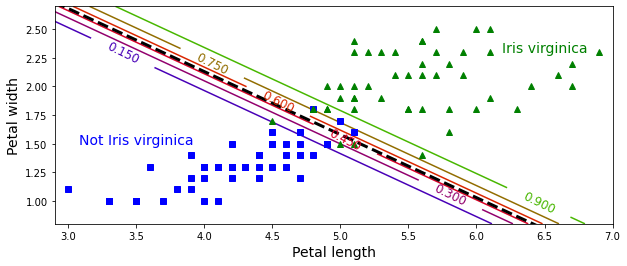
위 이미지는 데이터셋을 꽃잎 너비와 꽃잎 길이 두 개의 특성으로 보여준 것.
학습이 끝나면 logistic regression classifier가 이 두 특성을 기반으로하여
새로운 꽃이 iris-verginica인지 확률을 추정할 수 있다.
점선은 모델이 50% 확률 추정을 하는 지점으로, 이 모델의 decision boundary이다.
이 경계는 선형의 모습이다.
15%와 90%의 선들은 모델이 특정 확률로 출력하는 포인트를 나타냄.
모델은 맨 오른쪽 위의 꽃들을 90% 이상의 확률로 iris-virginica로 판단할 것임.
이 글의 내용은 많은 부분 아래 링크인 핸즈온 머신러닝 2판을 참고했으며
영리 목적이 아닌 개인적인 학습을 위해 정리한 내용을 바탕으로 작성했음을 밝힙니다.
내용 참고
https://book.naver.com/bookdb/book_detail.nhn?bid=16328592
핸즈온 머신러닝
머신러닝 전문가로 이끄는 최고의 실전 지침서 텐서플로 2.0을 반영한 풀컬러 개정판 『핸즈온 머신러닝』은 지능형 시스템을 구축하려면 반드시 알아야 할 머신러닝, 딥러닝 분야 핵심 개념과
book.naver.com
'딥러닝관련 > 기초 이론' 카테고리의 다른 글
| Cross entropy loss 정리 (0) | 2022.03.06 |
|---|---|
| 소프트맥스 회귀(softmax regression) (0) | 2022.03.06 |
| 규제가 있는 선형 모델 (0) | 2022.02.27 |
| 편향/분산 트레이드 오프 (Bias/variance trade-off) (0) | 2022.02.27 |
| 다항 회귀 (polynomial regression) (0) | 2022.02.21 |



