Polynomial Regression(다항 회귀)
다항... 다항....
다항의 의미는 한 개 이상의 항의 합으로 이루어진 식 이라고 표현한다.
https://ko.wikipedia.org/wiki/%EB%8B%A4%ED%95%AD%EC%8B%9D
다항식 - 위키백과, 우리 모두의 백과사전
수학에서, 다항식(多項式, 문화어: 여러마디식, 영어: polynomial)은 한 개 이상의 항의 합으로 이루어진 식이다. 즉, 단항식의 결합(덧셈과 뺄셈)으로 이루어진 식이다. 예를 들어, x2 - 2x + 3, 4x3, 5xy +
ko.wikipedia.org
기존에 보았던 식이 단항식 (y = ax) 와 같았다면 다항식은 여러 단항식의 조합으로 볼 수 있다.
(보통 다항 회귀에서는 2차.. 3차 n차 항까지 표현이 되는듯 하다)
그렇게되면 아무래도 다항 회귀가 단항 회귀보다 조금 더 복잡한 형태일 수 밖에 없다.
아래 코드를 보면 X에 대해서 제곱형태가 추가되어 다항식이 이루어졌다.
(아래 X가 제곱된 이유는 기존의 feature을 제곱하여 새로운 feature처럼 쓰이겠다는 말로 볼 수 있겠다)
# source code modified from https://github.com/rickiepark/handson-ml2/blob/master/04_training_linear_models.ipynb
import numpy as np
import numpy.random as rnd
import matplotlib.pyplot as plt
np.random.seed(8138)
m = 100
X = 6 * np.random.rand(m, 1) - 5
y = 4 * X**2 + X + 3 + np.random.randn(m, 1)
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([-5, 5, 0, 50])
plt.show()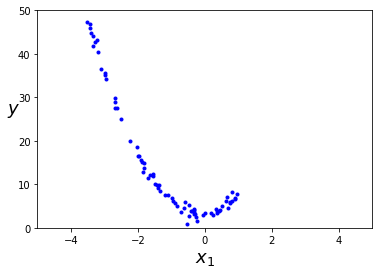
위와 같이 데이터가 비선형적으로 배치되어 있다면??
직선으로 구분하자고 하면 잘 구분되지 않을 것이다.
이 경우 PolynomialFeatures를 사용하여 데이터 변환한다.
이는 training set에 있는 각 feature를 제곱하여 새로운 특성으로 추가한다
# source code from https://github.com/rickiepark/handson-ml2/blob/master/04_training_linear_models.ipynb
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
X[0], X_poly[0]
# array([-2.67884132]), array([-2.67884132, 7.1761908 ])lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
lin_reg.intercept_, lin_reg.coef_
# (array([3.1361382]), array([[1.17226463, 4.02225781]]))원래 함수는 y = 4x^2 + x + 3 + 가우시안노이즈인데
예측 모델은 y = 4.022x^2 + 1.172x + 3.136으로 예측한 걸 알 수 있다.
X_new=np.linspace(-5, 5, 100).reshape(100, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, "b.")
plt.plot(X_new, y_new, "r-", linewidth=2, label="Preds")
plt.xlabel("$x_1$", fontsize=10)
plt.ylabel("$y$", rotation=0, fontsize=10)
plt.legend(loc="upper left", fontsize=10)
plt.axis([-5, 5, 0, 50])
plt.show()
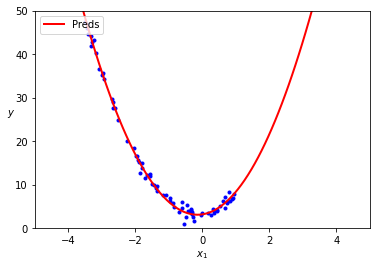
feature가 여러개일 때 polynomial regression은 features 사이의 관계를 찾을 수 있다.(일반적인 선형 모델은 어려움)
이 글의 내용은 많은 부분 아래 링크인 핸즈온 머신러닝 2판을 참고했으며
영리 목적이 아닌 개인적인 학습을 위해 정리한 내용을 바탕으로 작성했음을 밝힙니다.
내용 참고
https://book.naver.com/bookdb/book_detail.nhn?bid=16328592
'딥러닝관련 > 기초 이론' 카테고리의 다른 글
| 규제가 있는 선형 모델 (0) | 2022.02.27 |
|---|---|
| 편향/분산 트레이드 오프 (Bias/variance trade-off) (0) | 2022.02.27 |
| Mini-batch Gradient Descent(미니배치 경사 하강법) (0) | 2022.02.20 |
| Stochastic gradient descent(확률적 경사 하강법) (0) | 2022.02.20 |
| 경사 하강법(Gradient Descent) (0) | 2022.02.20 |



