2022.01.24 - [딥러닝관련/기초 이론] - 선형 회귀 (Linear Regression)
선형 회귀 (Linear Regression)
선형 회귀 모델 선형 회귀(Linear Regression)의 의미 수많은 점들을 설명할 수 있는 선을 그으려면 어떻게 해야 할까? 간단한 선형 회귀 모델 $$\textcolor{red}{\text{삶의 만족도} = θ_{0} + θ_{1} * \text{1..
better-tomorrow.tistory.com
본 글은 위로부터 이어짐 - 중요한 내용이라 따로 뺌
(책 내용 뿐 아니라 추가적인 내용도 취합하여 정리)
RMSE를 최소화하는 θ를 찾는 방법 2.
경사하강법(Gradient Descent)
여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘.
기본 아이디어
cost function을 최소화하기 위해 반복해서 파라미터를 조정해가는 것.
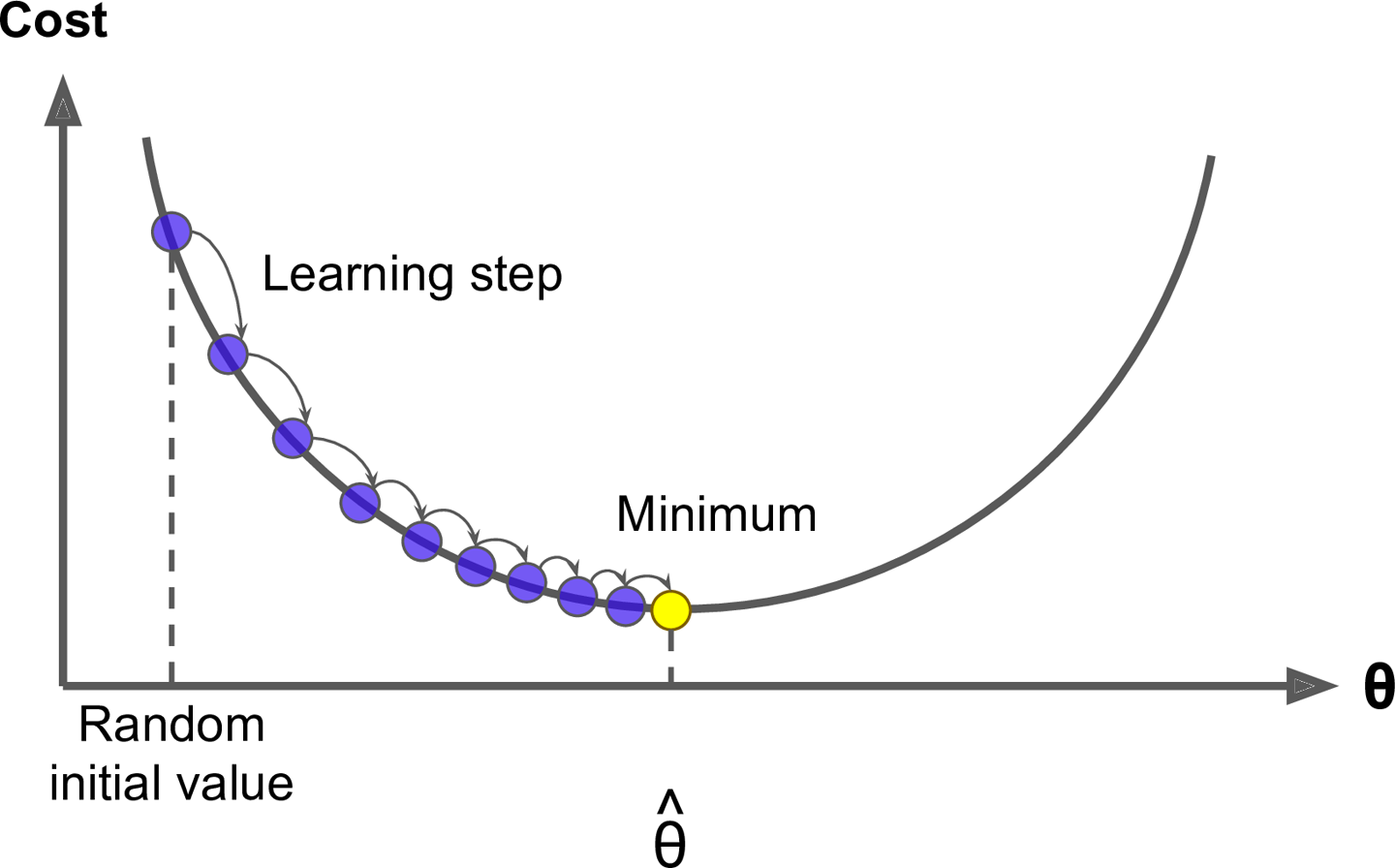
구체적으로 보면 θ를 임의의 값으로 시작해서(random initial value)
한 번에 조금씩 cost function이 감소되는 방향으로 진행하여
알고리즘이 최솟값에 수렴할 때까지 점진적으로 향상 시킴
위는 모델 파라미터가 무작위하게 초기화된 후 반복적으로 수정되어 cost function을 최소화한다.
학습 step 크기는 cost function에서의 기울기(gradient)에 비례한다.
(따라서, 파라미터가 최솟값에 가까워질수록 스템 크기가 점진적으로 줄어듦)
여기서 중요한 파라미터가 필요함.
바로 step의 크기로 learning rate라는 하이퍼 파라미터로 결정된다.
Learning rate가 너무 작으면 알고리즘이 수행하기 위해 반복을 많이 하므로 시간이 오래걸린다. - 아래 사진 참고
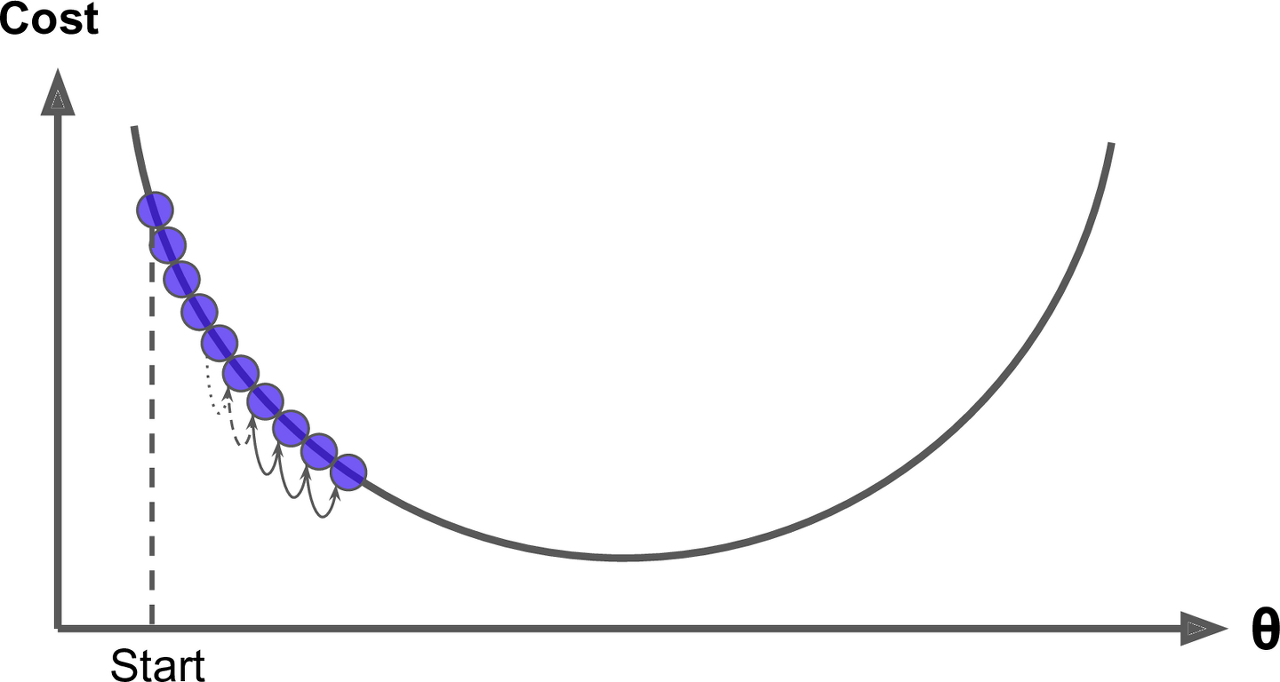
반면 learning rate가 너무 크면 반대편으로 튄다.
이는 알고리즘을 더 큰 값으로 발산하게되어 적절한 해법을 찾지 못함. - 아래 사진 참고

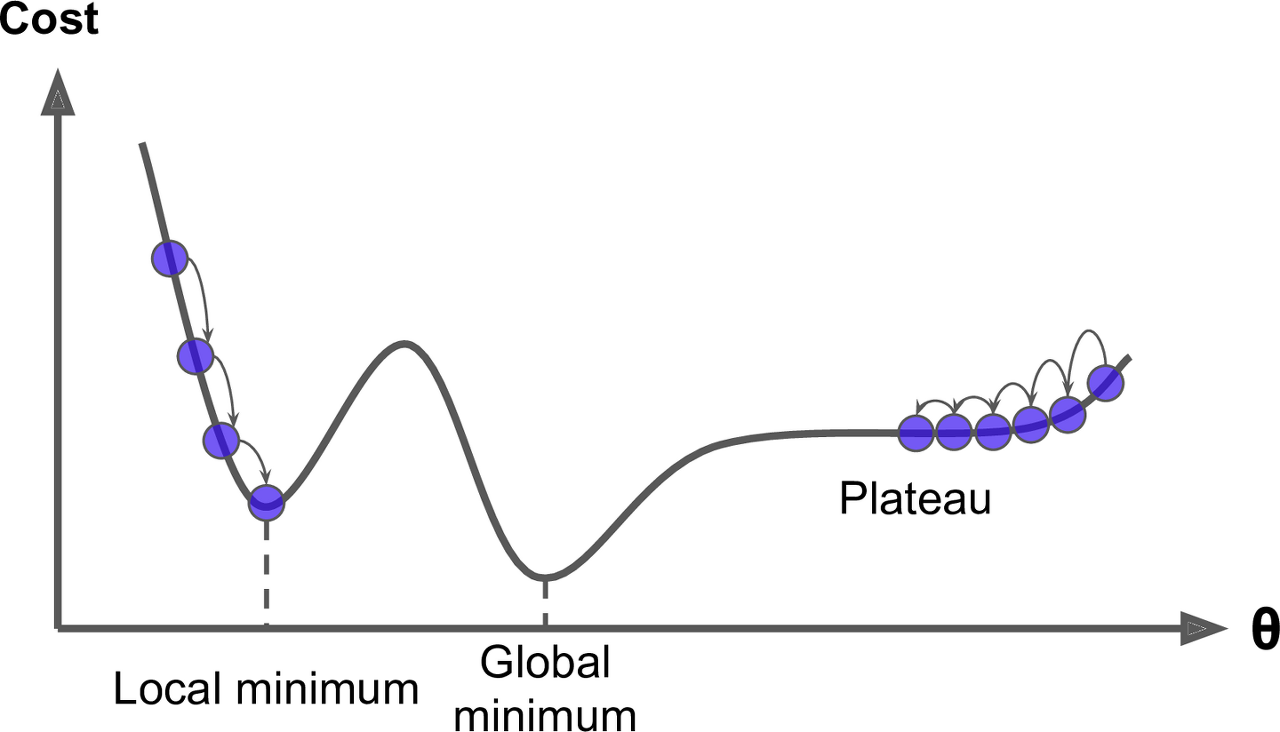
그러나 실제 환경에서는 모든 cost function이 매끈한 그릇과 같지는 않다.
holes, ridges, plateaus 등 특이한 지형이 있으면 최솟값으로 수렴하기 매우 어려움. - 아래 그림 참고
아래 그림을 보면 gradient descent의 두 가지 문제점을 확인 할 수 있다.
1.
Random initialization 때문에 알고리즘이 Global minimum이 아닌 local minimum에 빠질 수 있다.
(왼쪽에서 시작한 경우)
2.
평탄한 지역(plateau)을 지나기 위해 시간이 오래 걸리고 일찍 멈추게 되어 global minimum에 도달하지 못하게된다.
(오른쪽에서 시작한 경우)
MSE function의 경우, convex function(볼록 함수)
-> 이는 local minimum이 없고 하나의 global minmum만 있다는 뜻.
-> 또한 연속된 함수이며, gradient가 값자기 변하지 않는다.(립시츠 연속)
립시츠 연속(Lipschitz continuous)
어떤 함수의 도함수가 일정한 범위 안에서 변할 때 이 함수를 립시츠 연속 함수라고 함
(ex, 기울기가 일정한 범위내에 속해 있을 때)
특성들의 scale이 각기 다르면 cost function이 매우 길쭉한 모양일 수 있다.
아래는 특성의 스케일이 같을 때(왼쪽)와 다를 때(오른쪽)에 대한 gradient descent를 보여준다.
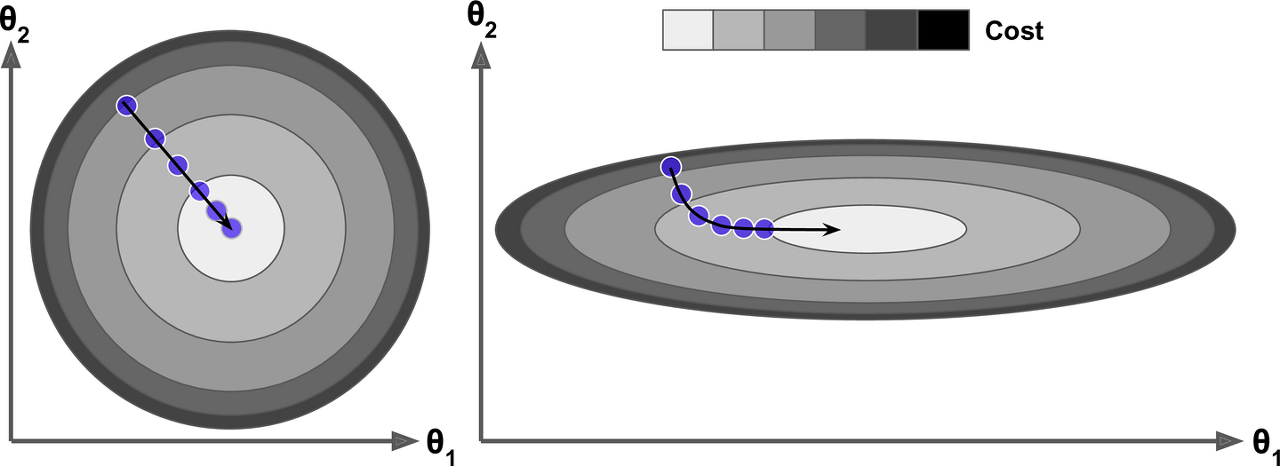
왼쪽의 그래프는 gradient descent algorithm이 최솟값으로 곧장 진행하고 있어 빠르게 도달한다.
반면, 오른쪽 그래프는 길게 돌아서 나간다.결국, 최솟값으로 가지만 시간이 오래 걸린다.
(스케일을 같게 한다 -> * Normalization의 중요성)
위 과정은 모델 학습이 cost function을 최소화하는 model parameter의 조합을 찾는 일임을 말한다.
이를 모델의 parameter space에서 찾는다라고 한다.
모델이 가진 파라미터가 많을수록 이 공간의 차원은 커지고 찾기가 더 어려워진다.
배치 경사 하강법(batch gradient descent)
경사하강법을 구현하려면 각 모델 파라미터 θ에 대해 비용 함수의 gradient를 계산해야 한다.
이는, θ가 조금 변경될 때 cost function이 얼마나 바뀌는지 계산해야 한다는 의미
이를 partial derivative(편미분, 편도함수)
위를 쉽게 생각하면,
"산에 오른 후, 동쪽을 밟았을 때 느껴지는 산의 기울기는?"
경사하강법으로 할 때 동&서&남&북을 모두 고려한다.
$$\text{아래 식은 파라미터} θ_{j} \text{에 대한 cost function의 편미분} \frac{\partial}{\partial θ_{j}} MSE(θ) $$
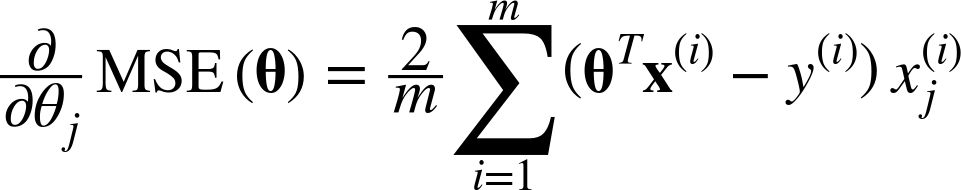
위와 같이 파라미터에 대한 도함수를 각각 계산하는 대신 아래와 같이 한꺼번에 계산할 수 있다.
이를 gradient vector라 하며(∇θMSE(θ)) 이는 cost function의 편미분 값들을 모두 가지고 있다.
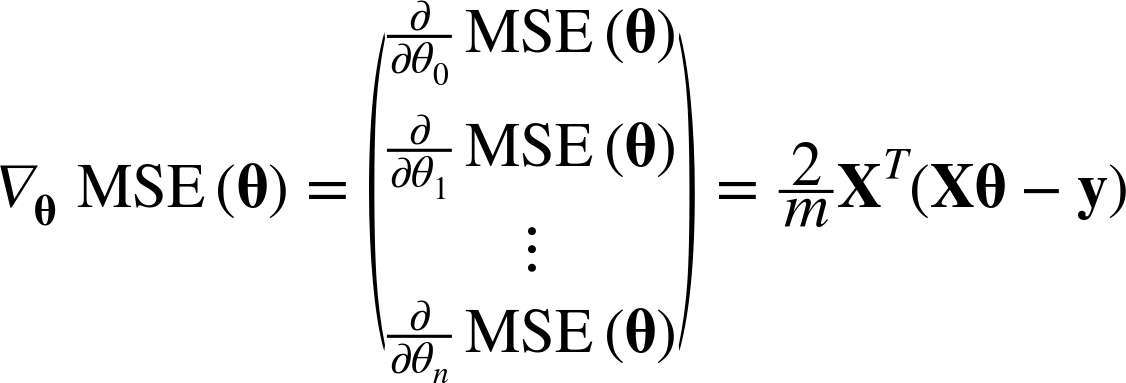
확인해야 할 점.
위를 잘 보면 X는 대문자로 되어 있다. 이는 전체 training set을 의미하며,
이는 매 gradient descent 시, 모든 trainind set에 대해 계산한다는 의미이다.
이런 이유로 데이터 수가 많으면 많을 수록 학습이 느려진다.
gradient descent는 특성의 수에 대해 민감하지 않는다.
따라서, 많은 특성의 데이터를 학습 시키려면 정규방정식이나 SVD 분해보다 gradient descernt를 사용하는 것이 훨씬 빠르다.
위 편미분한 식을 보면 분자에 2가 있는 것을 볼 수 있는데 이는 MSE 식을 미분했을 때 나오는 지수 2의 값이 곱해진 걸로 볼 수 있음.(실제 학습 할 때는 learning rate에 곱해지기 때문에 종종 1/2를 곱하여 간단하게 표현하기도 함)
만약 위로 향하는 gradient vector가 구해지면 반대 방향인 아래로 내려가야 한다.
즉, θ에서 ∇θMSE(θ)를 뺀다는 말.
여기서 learning rate η가 적용된다.
내려가는 스텝의 크기를 결정하기 위해 gradient vector에 η을 곱해준다.
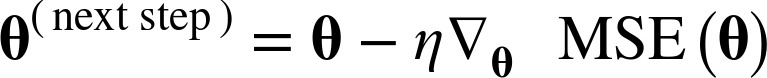
이 알고리즘을 구현해볼 수 있음
# original code from https://github.com/rickiepark/handson-ml2/blob/master/04_training_linear_models.ipynb
eta = 0.1 # 학습률
n_iterations = 1000
m = 100
theta = np.random.randn(2,1) # 랜덤 초기화
for iteration in range(n_iterations):
gradients = 2/m * X_b.T.dot(X_b.dot(theta) - y)
theta = theta - eta * gradients위 theta를 보면 찾고자하는 값에 가까운 것을 확인할 수 있다.

위 그림은 세 가지 다른 learning rate를 사용하여 진행한 gradient descent의 step 처음 10개
왼쪽의 경우 learning rate가 너무 낮음(최적점에 느리게 도착)중간의 경우 learning rate가 적절 (최적점에 삐르게 도착)오른쪽의 경우 learning rate가 너무 높음 (최적점에서 점점 멀어짐)
적절한 learning rate를 찾으려면 반복 횟수를 제한하여 grid search를 진행(그러나 실제로 모델이 크고 데이터 수가 많으면 grid search만 하는데도 시간이 너무 오래걸린다..._._)
책에서는 허용오차를 주고 gradient vector(vector의 norm)이 허용오차보다 작아지면gradient descent가 최솟값에 도달한 것이므로 알고리즘을 중지함.
다음 글
2022.02.20 - [딥러닝관련/기초 이론] - Stochastic gradient descent(확률적 경사 하강법)
Stochastic gradient descent(확률적 경사 하강법)
2022.02.20 - [딥러닝관련/기초 이론] - 경사 하강법(Gradient Descent) 경사 하강법(Gradient Descent) 2022.01.24 - [딥러닝관련/기초 이론] - 선형 회귀 (Linear Regression) 선형 회귀 (Linear Regression) 선..
better-tomorrow.tistory.com
이 글의 내용은 많은 부분 아래 링크인 핸즈온 머신러닝 2판을 참고했으며
영리 목적이 아닌 개인적인 학습을 위해 정리한 내용을 바탕으로 작성했음을 밝힙니다.
내용 참고
https://book.naver.com/bookdb/book_detail.nhn?bid=16328592
'딥러닝관련 > 기초 이론' 카테고리의 다른 글
| Mini-batch Gradient Descent(미니배치 경사 하강법) (0) | 2022.02.20 |
|---|---|
| Stochastic gradient descent(확률적 경사 하강법) (0) | 2022.02.20 |
| Swin Transformer (0) | 2021.11.25 |
| Vision Transformer (ViT) 정리 : An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale (0) | 2021.11.12 |
| Transformer 정리 (0) | 2021.11.09 |



