신경망 학습의 목적
Loss function의 값을 가능한 한 낮추는 parameter를 찾는 것.
Loss function의 값을 가능한 낮추기 위한 parameter의 최적값을 찾는 문제.
-> 최적화(optimization)
parameter의 기울기를 구해, 기울어진 방향으로
매개변수 값을 갱신하는 일을 몇 번이고 반복해서 최적의 값에 다가감.
최적화는 backpropagation 과정 중에 weight를 업데이트하면서 진행되는데,
이때
한 스텝마다 이동하는 발자국의 크기 (보폭)은 Learning Rate로 정의되고
앞으로 이동할 방향은 Gradient를 통해 정의된다
Gradient Descent
이전에 설명했던 바와 같이, Gradien Descent는
기울기를 활용해 함수의 손실 함수의 최솟값(또는 가능한 한 작은 값)을 찾는 방법이다.
1. 현재의 point에서 손실 함수의 1차 도함수인 gradient를 계산
2. 현재 지점에서 계산된 양만큼 증가된 gradient의 반대 방향으로 이동
Gradient Descent는 first-order iterative optimization 알고리즘이다.
(* optimization에서 first-order -> Gradient Descent가 parameter update를 수행할 때 1차 도함수만 고려한다는 의미)
Cost function 혹은 Loss function으로 표현되는 함수로 인해 나오는 결과 값을 최소화하기 위해,
cost function이 convex(볼록)한 경우, 가능한 global minimum을 찾는 것을 목표로 한다.
그러나, 많은 경우, objective function은 non-convex한 경향이 있어,
objective function의 가능한 낮은 값을 찾는 것이 적합한 solution으로 평가됨


이 아이디어는 Neural Network의 hidden layer를 통해 training set를 전달한 다음,
training set의 training sample을 사용하여 gradient를 계산하여 layer의 parameter를 업데이트 하는 것
→ 확률적 경사 하강법(SGD)
확률적 경사 하강법(Stochastic Gradient Descent)
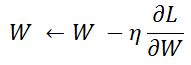
W : 갱신할 가중치 매개변수
∂L/∂W : W에 대한 손실 함수의 기울기
η : 학습률(learning rate)
← : 우변의 값으로 좌변의 값을 갱신한다.
기울어진 방향으로 일정 거리만 가겠다.
# pseudocode
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads): # params, grads -> dictionary type
for key in params.keys():
params[key] -= self.lr * grads[key]
network = TwoLayerNet(...)
optimizer = SGD()
for i in range(iterations):
...
x_batch, t_batch = get_mini_batch(...)
grads = network.gradienmt(x_batch, t_batch)
params = network.params
optimizer.update(params. grads)
...
SGD의 단점
SGD는 단순하고 구현도 쉽지만, 문제에 따라서는 비효율적일 때가 있음.
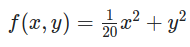
위와 같은 수식을 보면 아래와 같이 x축 방향으로 길게 늘어난 등고선 형태로 나타낼 수 있다.
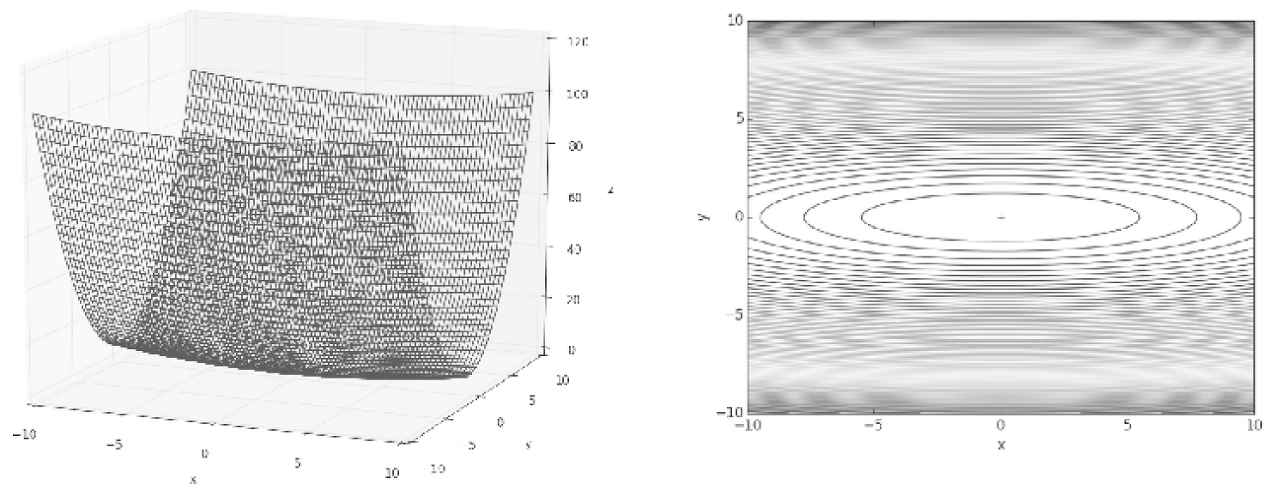
위 함수의 기울기를 그려보면 아래와 같이 표현 가능

위를 잘 보면
Y축 방향으로 기울기가 크고
X축 방향으로 기울기가 작다.
여기서 최솟값이 되는 위치는 (x, y) = (0, 0) 이지만
위 그림에서는 기울기가 대부분 (0, 0)을 가르키지 않는다.
해당 함수에 대해 SGD를 적용해 보자
초기값은 (x, y) = (-7.0, 2.0)
결과는 아래와 같이 탐색과정을 거친다

위 움직임을 보면 상당히 왔다갔다하는 움직임을 보여준다.
어찌보면 비효율적인 움직임으로 볼 수 있다.
즉, SGD의 단점은 비등방성 함수에서는 탐색 경로가 비효율적이라는 것.
(*비등방성 함수 : 방향에 따라 성질, 즉 기울기가 달라지는 함수)
위와 같은 이유로 아래와 같은 최적화 알고리즘의 필요성이 생겨남
1. 무작정 기울어진 방향으로 진행하는 단순한 방식보다 더 영리한 묘안이 필요해짐
2. 지그재그로 탐색하는 근본 원인은 기울어진 방향이 본래의 최솟값과 다른 방향을 가리켜서라는 점.
===============================================
추가적으로 내용을 덧붙이자면
Batch Gradient Descent
* batch는 total training dataset을 의미한다.
-> 전체 데이터에 대해서 loss를 구한 뒤 gradient를 한 번만 계산하여 학습을 진행한다.
모든 training data는 고려하여 single step을 수행
모든 training examples의 gradient의 평균을 취한 다음, 그 mean gradient를 사용하여 parameter를 업데이트,
(1 iteration -> 1 epoch)

위 그래프는 Batch Gradient Descent 시 cost의 변화를 나타낸 것이며,
single step에 대한 training data의 모든 기울기에 대해 평균을 내고 있기 때문에 매우 smooth 하다.
장점
1. 전체 데이터셋에 대해 weight update가 한 번만 이뤄지기 때문에 SGD보다 업데이트 횟수가 적음.
2. 전체 데이터에 대해 gradient를 계산하기 때문에 optimal로의 수렴이 안정적으로 진행된다.
3. 병렬 처리의 이점을 잘 살릴 수 있다고 함
단점
1. Training time이 너무 오래 걸린다.
2. 전체 dataset에 대한 손실함수의 값을 업데이트 전까지 보관해야 하기 때문에 메모리 소모가 많이 필요하다.
3. Local minimum에 빠지면 나오기가 힘들다.
Stochastic Gradient Descent
Batch Gradient Descent를 적용한다고 가정해보자,
만약 내가 가지고 있는 데이터의 수가 총 500만개이다.
이 500만개를 한꺼번에 gradient를 계산하여 weight update하는 것은 효율적인 방법이 아니다.
이러한 단점을 해결하기 위해 stochastic gradient descent 방법을 사용한다.
stochastic gradient descent는 한 번에 한 가지 example만 고려하여 single step을 수행한다.
1. example을 랜덤으로 뽑아 준비한다.
2. Neural Network에 feed-forward
3. gradient를 계산
4. 계산한 gradient를 사용하여 weight update
한 번에 하나의 example만 고려하기 때문에 training examples들에 따라 cost의 변동이 심할 수 있다.
장점
1. Batch gradient descent보다 gradient가 크게 변화하기 때문에, local minimum을 탈출할 수 있다.
2. Update step에 걸리는 시간이 짧기 때문에 수렴속도가 상대적으로 빠르다.
단점
1. 좋은 solution을 줄 수 있지만 optimal하지 않을 수 있다.
2. 병렬 처리의 이점을 활용할 수 없음
Mini-batch Gradient Descent
Batch Gradient descent는 최소값으로 직접 수렴할 수 있으며,
Stochastic gradient descent는 더 큰 데이터 세트에 대해 빠르게 수렴할 수 있음.
하지만 SGD에서는 한 번에 하나의 sample만 사용하기 때문에 vector화하여 구현할 수가 없다.
이렇게 되면 computation 속도가 느려질 수 있다.
이를 위해 Batch Gradient Descent와 SGD가 혼합되어 사용된다.
실제 데이터 세트보다 적은 고정된 수의 training set batch를 사용하고 이를 mini-batch라고 표현
이렇게 하면 이전에 본 두 가지 변형의 장점을 모두 달성하는 데 도움
Fixed size의 mini-batch를 만든 후 다음 단계 수행
1. Pick a mini-batch
2. Neural Network에 feed-forward
3. Mini-batch의 mean gradient 계산
4. mean gradient를 사용하여 gradient를 업데이트
모멘텀(momentum)
Momentum : 운동량을 뜻하는 단어.

W : 갱신할 가중치 매개변수
∂L/∂W : W에 대한 손실 함수의 기울기
η : 학습률(learning rate)
v : 물리에서 말하는 속도(velocity)
αv : 물체가 아무런 힘을 받지 않을 때 서서히 하강시키는 역할
(α : 0.9 등으로 설정)
← : 우변의 값으로 좌변의 값을 갱신한다.

기울기 방향으로 힘을 받아 물체가 가속된다는 물리 법칙
# pseudocode
class Momentum:
def __init__(self, lr = 0.01, momentum = 0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_list(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * self.grads[key]
self.params[key] += self.v[key]Momentum의 움직임은 아래와 같다.

x축의 힘은 아주 작지만 방향은 변하지 않아 한 방향으로 일정하게 가속
y축의 힘은 크지만 위아래로 번갈아 받아서 상충하여 y축 방향의 속도는 안정적이지 않음
전체적으로는 SGD보다 x축 방향으로 빠르게 다가가 지그재그 움직임이 줄어든다.
AdaGrad
신경망 학습에서는 Learning rate 값이 중요.
너무 작으면 학습이 길어지고
너무 크면 발산한다.
이 Learning rate를 정하는 효과적 기술로 learning rate decay가 있다.
학습을 진행해가면서 learning rate를 줄여가는 방법
AdaGrad는 '각각의' 매개변수에 '맞춤형' 값을 만들어준다.
개별 매개변수에 adaptive하게 learning rate를 조정하면서 학습을 진행


수식은 위와 같다.
W : 갱신할 가중치 매개변수
∂L/∂W : W에 대한 손실 함수의 기울기
η : 학습률(learning rate)
h : 기존 기울기 값을 제곱하여 계속 더해준다.(⊙ -> 원소별 곱셈)
← : 우변의 값으로 좌변의 값을 갱신한다.
매개변수를 갱신할 때 1/root(h)를 곱해 learning rate를 조정한다.
매개변수의 원소 중에서 많이 움직인(크게 갱신된) 원소는 learning rate가 낮아진다.
(Learning rate 감소가 매개변수의 원소마다 다르게 적용됨)
class AdaGrad:
def __init__(self, lr = 0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
AdaGrad는 과거의 기울기를 제곱하여 계속 더해감
그래서 학습을 진행할수록 갱신 강도가 약해짐실제로 무한히 계속 학습하면 어느 순간 갱신량이 9이 되어 전혀 갱신되지 않는다.
이 문제를 해결하기 위해 RMSprop이라는 방법이 존재
RMSprop은 과거의 모든 기울기를 균일하게 더해가는 것이 아니라,
먼 과거의 기울기는 서서히 잊고 새로운 기울기 정보를 크게 반영.(지수이동평균)
# pseudocode
class AdaGrad:
def __init__(self, lr = 0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
================================================
위 코드의 마지막 줄을 보면 1e-7이라는 아주 작은 값을 더하는 부분이 있음.
이는 self.h[key]에 0이 담겨 있다 해도 0으로 나누는 사태를 막아줌.
(학습 시 하이퍼파라미터로 설정 가능하다)
================================================
AdaGrad의 움직임은 아래와 같다.

위 그림을 보면 최솟값을 향해 효율적으로 움직이는 것을 알 수 있음.
y축 방향은 기울기가 커서 처음에는 크게 움직이지만, 그 움직임에 비례해 갱신 정도도 큰 폭으로 작아지도록 조정.
그래서 y축 방향으로 갱신 강도가 빠르게 약해지고 지그재그 움직임이 줄어듦.
Adam
Mementum은 공이 그릇 바닥을 구르는 듯한 움직임을 보였음

AdaGrad는 매개변수의 원소마다 적응적으로 갱신 정도를 조정했음.

이 두 기법을 융합한다면??????
(momentum + AdaGrad) ------> Adam

Adam의 갱신 과정도 그릇 바닥을 구르듯 움직인다.
Momentum과 비슷한 패턴이지만, Momentum 때보다 공의 좌우 흔들림이 적다.
이는 학습의 갱신 강도를 adaptive하게 조정해서 얻는 혜택.
Adam은 hyper-parameter로
Learning rate
β_1 (일차 모멘텀용 계수)
β_2 (이차 모멘텀용 계수)
를 사용한다.
내용 참고
book.naver.com/bookdb/book_detail.nhn?bid=11492334
밑바닥부터 시작하는 딥러닝
직접 구현하고 움직여보며 익히는 가장 쉬운 딥러닝 입문서!『밑바닥부터 시작하는 딥러닝』은 라이브러리나 프레임워크에 의존하지 않고, 딥러닝의 핵심을 ‘밑바닥부터’ 직접 만들어보며
book.naver.com
옵티마이저 Optimizer 정복기 (부제: CS231n Lecture7 Review)
딥러닝을 처음 공부할 때 주춤하게 되는 지점이 바로 이 옵티마이저 파트이다. 개인적 경험상 여러번 반복해서 공부하였고, 어느 정도 이해하는데에 꽤나 긴 시간이 소요되었다. 따라서 이 글을
velog.io
https://towardsdatascience.com/batch-mini-batch-stochastic-gradient-descent-7a62ecba642a
Batch, Mini Batch & Stochastic Gradient Descent
An introduction to gradient descent and it’s variants.
towardsdatascience.com
https://light-tree.tistory.com/133
딥러닝 용어정리, MGD(Mini-batch gradient descent), SGD(stochastic gradient descent)의 차이
제가 공부한 내용을 정리한 글입니다. 제가 나중에 다시 볼려고 작성한 글이다보니 편의상 반말로 작성했습니다. 잘못된 내용이 있다면 지적 부탁드립니다. 감사합니다. MGD(Mini-batch gradient descen
light-tree.tistory.com
Difference between Batch Gradient Descent and Stochastic Gradient Descent - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
https://towardsdatascience.com/gradient-descent-811efcc9f1d5
'딥러닝관련 > 기초 이론' 카테고리의 다른 글
| 선형(linear) vs 비선형(non-linear) (4) | 2021.11.05 |
|---|---|
| Squeeze-and-Excitation Networks(SENET) (0) | 2021.10.19 |
| 신경망 정리 10-2 (오차 역전파 활성화 함수 계층 구현, Sigmoid) (0) | 2021.07.19 |
| 신경망 정리 10-1 (오차 역전파 활성화 함수 계층 구현, ReLU) (0) | 2021.06.13 |
| 특이값 분해 (singular decomposition) (0) | 2021.06.04 |



