경사법(gradient method)
기울기를 활용해 함수의 손실 함수의 최솟값(또는 가능한 한 작은 값)을 찾으려는 것이 경사법
그러나, 기울기가 가리키는 곳에 정말 함수의 최솟값이 있는지, 즉 그쪽이 정말로 나아갈 방향인지는 보장할 수 없다.
실제로 복잡한 함수에서는 기울기가 가리키는 방향에 최솟값이 없는 경우가 대부분.
함수가 극솟값, 최솟값, 또 안장점이 되는 곳에서는 기울기가 0
극솟값 : 국소적인 최솟값, 한정된 범위에서의 최솟값
경사법은 기울기가 0인 장소를 찾지만 그것이 반드시 최솟값이라고는 할 수 없다.
(극솟값이나 안장점일 가능성도 있음)
또 복잡하고 찌그러진 모양의 함수라면 대부분 평평한 곳으로 파고들면서 고원(plateau)라고 하는, 학습이 진행되지 않는 정체기에 빠질 수 있다.
기울어진 방향이 꼭 최솟갑을 가리키는 것은 아니나, 그 방향으로 가야 함수의 값을 줄일 수 있다.
그래서 최솟값이 되는 장소를 찾는 문제에서는 기울기 정보를 단서로 나아갈 방향을 정해야 한다.
경사법(gradient method)
경사법은 현 위치에서 기울어진 방향으로 일정 거리만큼 이동한다.
그런 다음 이동한 곳에서도 마찬가지로 기울기를 구하고, 또 기울어진 방향으로 나아가는 일을 반복
경사법은 기계학습의 최적화 문제에서 흔히 쓰는 방법
경사법은 최솟값을 찾느냐, 최대값을 찾느냐에 따라 이름이 다르다.
전자 : 경사 하강법 (gradient descent method)
후자 : 경사 상승법 (gradient ascent method)
일반적으로 신경망(딥러닝) 분야에서의 경사법은 '경사 하강법'으로 등장할 때가 많다.
경사법 수식

위 식은 파라미터를 갱신하는 양을 나타냄.
여기서 에타(eta η)는 학습률(learning rate를 나타낸다)
즉 매개변수 값을 얼마나 갱신하느냐를 정한다.
위를 반복하면서 변수를 계속 줄여나가며 함수의 값을 줄이는 것.
학습률 값은 0.01이나 0.001 등 미리 특정한 값으로 정해두어야 한다.
일반적으로 너무 크거나 작으면 '좋은 장소'를 찾아갈 수 없다.
아래는 경사 하강법 구현
import numpy as np
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h) 계산
x[idx] = tmp_val + h # 편미분 구할 변수의 변화량만 검사
fxh1 = f(x)
# f(x-h) 계산
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 값 복원
return grad
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
gradient_descent 함수의 인자들을 보면
f는 : 최적화하려는 함수
init_x : 초깃값
lr : learning rate,
step_num : 경사법에 따른 반복회수
numerical_gradient(f, x) : 함수의 기울기
step_num : 그 기울기에 학습율을 곱한 값으로 갱신하는 처리
예시
경사 하강법으로 아래 식의 최솟값 계산

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def _numerical_gradient_no_batch(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h) 계산
x[idx] = float(tmp_val) + h
fxh1 = f(x)
# f(x-h) 계산
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 값 복원
return grad
def numerical_gradient(f, X):
if X.ndim == 1:
return _numerical_gradient_no_batch(f, X)
else:
grad = np.zeros_like(X)
for idx, x in enumerate(X):
grad[idx] = _numerical_gradient_no_batch(f, x)
return grad
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append( x.copy() )
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
def function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])
lr = 0.1
step_num = 20
x, x_history = gradient_descent(function_2, init_x, lr=lr, step_num=step_num)
plt.plot( [-5, 5], [0,0], '--b')
plt.plot( [0,0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()

위에서는 초깃값을 (-3.0, 4.0)으로 설정한 후 경사법을 사용한다.
위 결과를 보면 결과적으로 x가 0에 가까워지는 것을 알 수 있다.
학습률을 0.1에서 10으로 설정하면 아래와 같이 값이 발산하는 것을 알 수 있다.
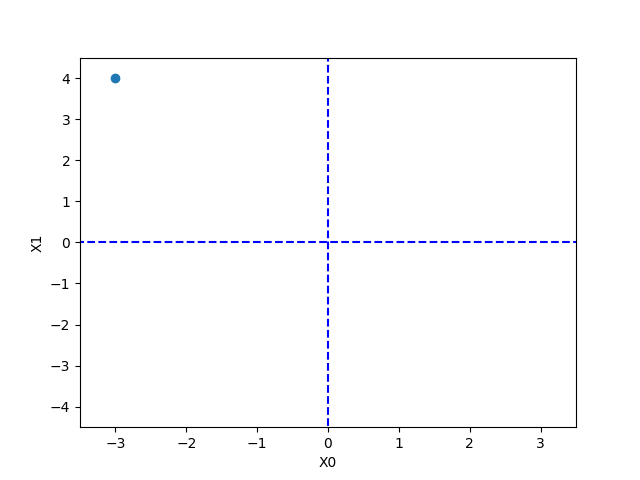
또 값이 너무 작으면 파라미터가 거의 갱신되지 않은채 끝이 난다.
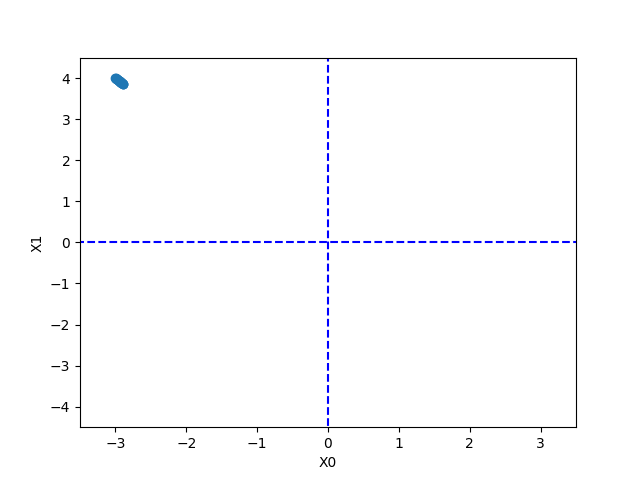
학습률과 같은 매개변수를 하이퍼파라미터
신경망의 가중치 매개변수는 훈련 데이터와 학습 알고리즘에 의해서 '자동'으로 획득되는 매개변수인 반면
학습률과 같은 하이퍼파라미터는 사람이 직접 설정해야 하는 매개변수.
신경망에서의 기울기
신경망 학습에서도 기울기를 구해야 함.
여기서의 기울기란 가중치 매개변수에 관한 손실 함수의 기울기
예를 들어 형상이 2 x 3. 가중치가 W, 손실 함수가 L인 신경망.
이 경우 아래와 같이 기울기를 표현할 수 있음
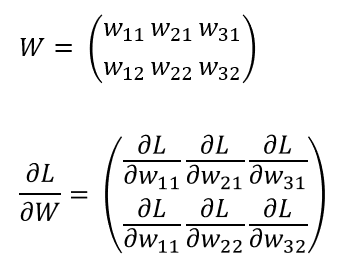
L에 대한 W의 편미분의 각 원소는 각각의 원소에 관한 편미분.
∂L/w_11은 w_11을 조금 변경했을 때 손실 함수 L이 얼마나 변화하느냐를 나타냄.
여기서 중요한 점 ∂L/W의 shape이 W의 shape과 같다는 것.
신경망 경사하강법 예시
# coding: utf-8
import sys, os
import numpy as np
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 값 복원
it.iternext()
return grad
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # 오버플로 대책
return np.exp(x) / np.sum(np.exp(x))
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 훈련 데이터가 원-핫 벡터라면 정답 레이블의 인덱스로 반환
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
class simpleNet:
def __init__(self):
self.W = np.array([[0.47355232, 0.9977393, 0.84668094],
[0.85557411, 0.03563661, 0.69422093]])
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
print("dW")
print(dW)
# 추가 확인
print("net.W")
print(net.W)
p = net.predict(x)
print(np.argmax(p))
print("loss")
print(net.loss(x, t))결과
dW
[[ 0.21924757 0.14356243 -0.36281 ]
[ 0.32887136 0.21534364 -0.544215 ]]
net.W
[[0.47355232 0.9977393 0.84668094]
[0.85557411 0.03563661 0.69422093]]
2
loss
0.9280682857864075
simpleNet 클래스는 형상이 2 x 3인 가중치 매개변수 하나를 인스턴스 변수로 갖는다.
해당 클래스는 메서드가 2개
1) predict(x) : 예측을 수행하는 메서드
2) loss(x, t) : 손실 함수의 값을 구하는 메서드
(x는 입력, t는 정답)
numerical_gradient(f, x)로 기울기 계산
f : 함수
x : f의 인수
=> 여기서는 net.W를 인수로 받아 손실 함수를 계산하는 새로운 함수 f를 정의
그리고 이 새로 정의한 함수를 numerical_gradient(f, x)에 넘긴다.
dW는 numerical_gradient(f, net.W)의 결과로, 형상은 2 x 3의 2차원 배열.
dW의 내용을 보면, w11은 대략 0.2(0.21924757)
이는 w_11을 h만큼 늘리면 손실 함수의 값은 0.2h만큼 증가한다는 의미
마찬가지로, w_23은 대략 -0.5(-0.544215), 이는 w_23을 h만큼 늘리면 손실 함수의 값은 0.5h만큼 감소하는 것.
손실함수를 줄인다는 관점에서는 w_11은 음의 방향으로, w_23은 양의 방향으로 갱신해야 함을 알 수 있다.
또한, w_11보다 w_23이 갱신되는 양이 더 크게 기여한다는 사실을 알 수 있다.
내용 참고
book.naver.com/bookdb/book_detail.nhn?bid=11492334
'딥러닝관련 > 기초 이론' 카테고리의 다른 글
| 신경망 정리 7 (학습 알고리즘 구현) (0) | 2021.05.29 |
|---|---|
| 기초 행렬 이론 정리 (0) | 2021.05.27 |
| 신경망 정리 5 (수치 미분, 편미분) (0) | 2021.05.23 |
| 신경망 정리 4 (손실 함수 설정) (0) | 2021.05.23 |
| 신경망 정리 3 (신경망 학습, MSE, Cross entropy loss ....) (0) | 2021.05.12 |


