jonathan-hui.medium.com/gan-wasserstein-gan-wgan-gp-6a1a2aa1b490
GAN — Wasserstein GAN & WGAN-GP
Training GAN is hard. Models may never converge and mode collapses are common. To move forward, we can make incremental improvements or…
jonathan-hui.medium.com
위 내용을 참고하여 정리하였습니다.
Earth-Mover(EM) distance/ Wasserstein Metric

왼쪽에 있는 박스들을 오른쪽으로 옮기려고 가정합니다.
1번 박스를 오른쪽 7번 location으로 옮깁니다.
여기서 moving cost는 weights x distance가 됩니다.
박스 1의 weight가 1로 설정한다면, moving cost는 6(7-1)이 됩니다.
아래와 같이 두 개의 moving plan이 있다고 가정합니다.

예를 들어, 첫 번째 plan에서, 우리는 두 개의 박스(2, 3)를 1에서 10으로 옮깁니다.
이러면 entry γ(1, 10)은 2가 됩니다.
(1번 장소에 있는 두 개의 박스(2와 3)를 10번 장소로 옮겼기 때문에 γ(1, 10) = 2)
그러면 첫 번째의 총 transport cost는 42가 됩니다.
도출
1번 박스 : 1번 장소 -> 7번 장소(γ(1, 7) -> cost 6)
2번 박스 : 1번 장소 -> 10번 장소(γ(1, 10) -> cost 9)
3번 박스 : 1번 장소 -> 10번 장소(γ(1, 10) -> cost 9)
4번 박스 : 2번 장소 -> 8번 장소(γ(2, 8) -> cost 6)
5번 박스 : 3번 장소 -> 9번 장소(γ(3, 9) -> cost 6)
6번 박스 : 3번 장소 -> 9번 장소(γ(3, 9) -> cost 6)
총 cost는 42가 됩니다.
하지만 모든 transport plan이 동일한 cost을 부담하는 것은 아닙니다.
Wasserstein distance (또는 EM distance)는 가장 저렴한 transport plan의 비용입니다.
아래 예에서 두 계획 모두 비용이 다르고 Wasserstein 거리 (최소 비용)는 2입니다.
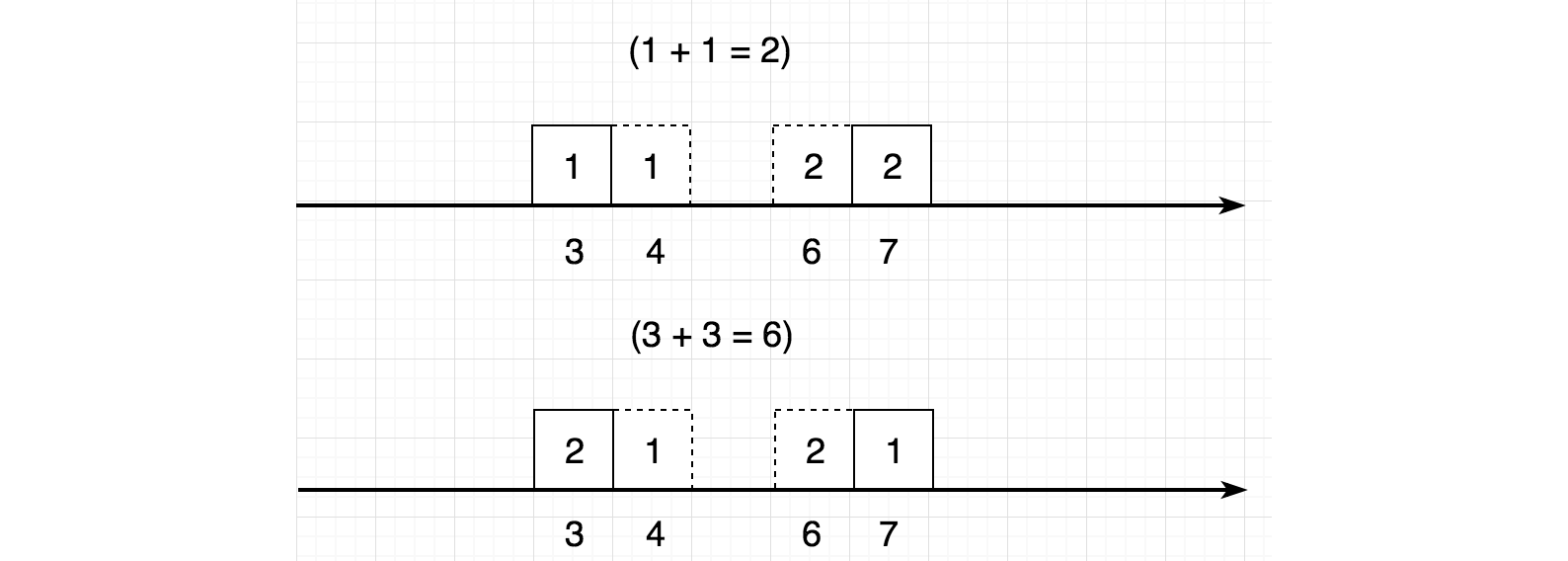
Wasserstein distance는 데이터 분포 $q$를 데이터 분포 $p$로 변환 할 때 확률질량(mass라고 표현)을 운반하는 최소 비용입니다.
Real data distribution $P_r$ 및 generated data distribution $P_g$에 대한 Wasserstein distance는
수학적으로 모든 transport plan (즉, 가장 저렴한 계획의 비용)에 대한 최대 하한 (infimum)으로 정의됩니다.
(즉, 생성된 분포가 실제 분포와 유사하게 만드는데 필요한 최소 distance를 계산)
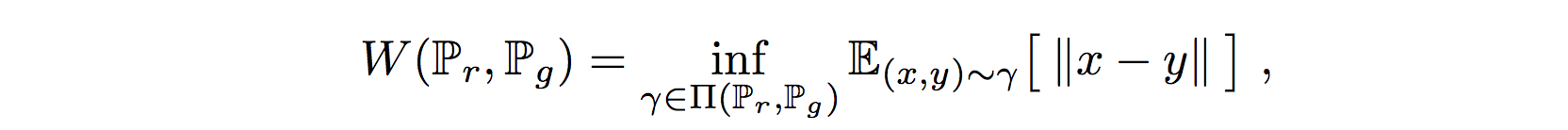
Π (Pr, Pg)는 marginals(주변 분포) 가 각각 Pr 및 Pg 인 모든 결합 분포(joint distribution) γ (x, y)의 집합을 나타냅니다.
----------------------------------------------------------------------------------------------------------------------------------
이산확률변수(discrete probability variable)가 두 개 일때, 이를 표현하는 방법
두 개의 이산확률변수 X, Y가 있을 때 이 둘의 결합확률분포는 다음과 같음
- $X$에서 임의의 값 $x$와 $Y$에서 임의의 값 $y$가 동시에 나타날 확률을 나타내는 함수를 결합확률함수
- 두 이산확률변수의 결합확률분포(joint probability distribution)로부터 각각의 이산확률변수에 대한 분포를 구할 수 있음
- 이를 주변확률분포라고 함
- Y가 가질 수 있는 모든 값들의 결합함수의 합은 확률 변수 X의 주변확률, 그 확률을 나타내는 함수를 주변확률 함수
|
|
x = 1 |
x = 2 |
x = 3 |
x = 4 |
|
y = 1 |
1/8 |
1/16 |
1/32 |
1/32 |
|
y = 2 |
1/16 |
1/8 |
1/32 |
1/32 |
|
y = 3 |
1/16 |
1/16 |
1/16 |
1/16 |
|
y= 4 |
1/4 |
0 |
0 |
0 |
X의 주변확률분포 P(X) = 1/2, 1/4, 1/8, 1/8 이다.
첫 번째값 1/2은 x=1로 고정된 상태에서 y가 1, 2, 3, 4일 때 각 값을 모두 더한값.
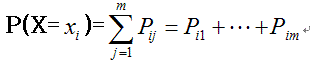
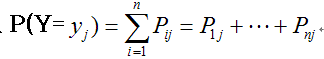
출처 : blog.daum.net/jchern/13756762
marginal probability distribution(주변확률분포)
일반적으로 확률(probability)이라 함은 나타날수 있는 가능성을 의미한다. 쉬운 예로 주사위를 던졌을때 각 눈이 나올 확률은 1/6이다. 그러면 확률 변수는 무엇인가 임의의 실험에 의해 값이 결정
blog.daum.net
----------------------------------------------------------------------------------------------------------------------------------
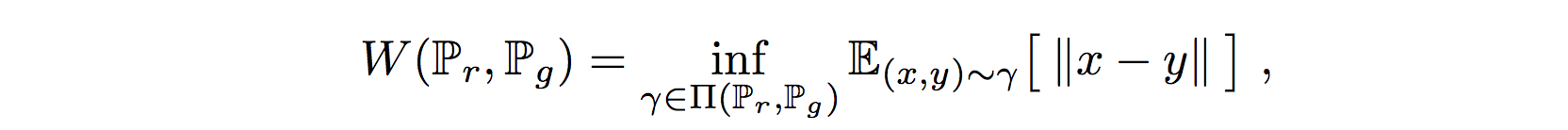
- 위의 equation은 continous space에서 example과 동일
- Π는 가능한 모든 transport plan γ을 포함합니다.

변수 $x$와 $y$를 결합하여 결합 분포(joint distribution) γ (x, y) 형성합니다.
그리고 γ (1, 10)은 단순히 위치 1에서 위치 10에있는 상자 수입니다.
위치 10에있는 상자의 수는 원래 임의의 위치에서 나와야합니다. 즉, ∑ γ (*, 10) = 2입니다.
이는 γ (x, y)에 각각 marginal $P_r$ 및 $P_g$가 있어야한다는 말과 같습니다.
KL-Divergence and JS-Divergence


여기서 $p$는 real data distribution이고
$q$는 모델에서 추정된 분포입니다.
가우시안 분포라고 가정 해 봅시다.
아래 다이어그램에서 $p$와 다른 평균을 갖는 몇 개의 $q$를 플로팅합니다.

$p$와 $q$ 사이의 해당 KL-divergence와 JS-divergence를 계산하고 0에서 35 사이의 평균 범위로 플로팅합니다.
예상대로 p와 q가 모두 같으면 divergence은 0입니다.
q의 평균이 증가하면 divergence가 증가합니다.
Divergence의 gradient는 결국 감소합니다.
기울기가 0에 가까웠습니다. 즉, 생성기는 기울기 하강에서 아무것도 배우지 않습니다.

실제로 GAN은 generator보다 쉽게 discriminator를 최적화 할 수 있습니다.
최적의 discriminator로 GAN object function을 최소화하는 것은 JS-divergence (증거)을 최소화하는 것과 같습니다.
위에서 설명한 것처럼 생성된 이미지의 분포 q가 Ground Truth p에서 멀리 떨어진 경우 generator는 거의 아무것도 학습하지 않습니다.
Arjovsky et al 2017은 GAN 문제를 수학적으로 설명하는 논문을 작성하여 다음과 같은 결론을 내렸습니다.
- Optimal discriminator는 generator가 개선 할 수 있는 좋은 정보를 생성합니다. 그러나 generator가 아직 제대로 작동하지 않으면 generator의 gradient가 감소하고 generator는 아무것도 학습하지 않습니다.

- 원래의 GAN 논문은 이러한 gradient vanishing problem을 해결하기 위해 대체 cost function를 제안합니다. 그러나 Arjovsky는 새로운 functions가 모델을 불안정하게 만드는 large variance of gradients를 가지고 있음을 보여줍니다.

- Arjovsky는 모델을 안정화하기 위해 생성 된 이미지에 노이즈를 추가 할 것을 제안합니다.

Wasserstein Distance
- 위에서 노이즈를 추가하는 방법 대신 Wasserstein GAN (WGAN)은 모든 곳에서 더 부드러운 기울기를 갖는 Wasserstein distance를 사용하는 새로운 비용 함수를 제안합니다.
- WGAN은 generator가 작동하는지 여부에 관계없이 학습합니다.
- 아래 다이어그램은 GAN 및 WGAN 모두에 대한 D (X) 값에 대한 유사한 플롯을 반복합니다.
- GAN (빨간색 선)의 경우 감소하거나 폭발하는 그라디언트로 영역을 채 웁니다.
- WGAN (파란색 선)의 경우 그라디언트가 모든 곳에서 더 매끄럽고 생성기가 좋은 이미지를 생성하지 않는 경우에도 더 잘 학습합니다.

Wasserstein GAN
그러나 Wasserstein distance에 대한 방정식은 매우 다루기 어렵습니다.
Kantorovich-Rubinstein 이중성을 사용하여 계산을 단순화하여
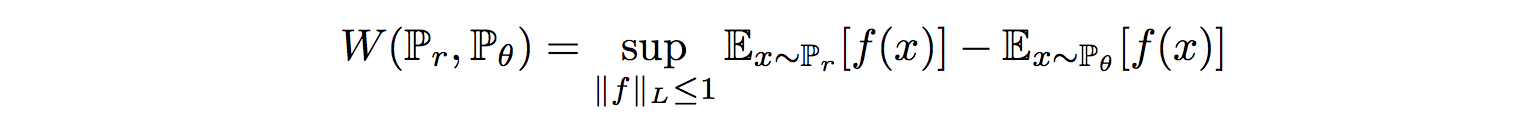
여기서 $sup$는 최소 상한(least upper bound)이고 $f$는이 제약을 따르는 1-Lipschitz 함수입니다

따라서 Wasserstein 거리를 계산하려면 1-Lipschitz 함수를 찾아야합니다.
다른 딥러닝 문제와 마찬가지로, 이를 학습하기 위해 딥 네트워크를 구축 할 수 있습니다.
실제로 이 네트워크는 sigmoid 함수없이 Discriminator $D$와 매우 유사하며 확률이 아닌 스칼라 score를 출력합니다.
이 점수는 입력 이미지가 얼마나 real인지로 해석 될 수 있습니다.
새로운 역할을 반영하기 위해 Discriminator를 critic로 이름을 바꿉니다.
GAN
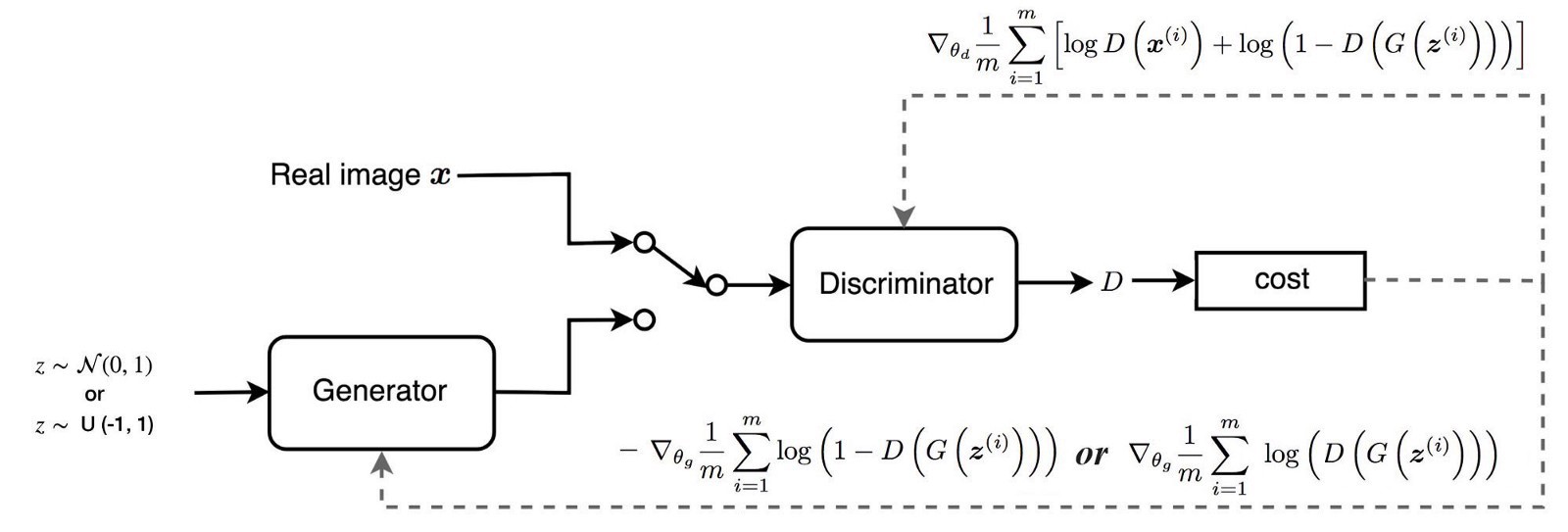
WGAN

네트워크 설계는 critic이 output sigmoid function을 가지고 있지 않다는 점을 제외하면 거의 동일합니다. 주요 차이점은 cost function에만 있습니다.

그러나 한 가지 중요한 것이 누락되었습니다.
$f$는 1-Lipschitz 함수여야합니다.
제약을 적용하기 위해 WGAN은 f의 최대 가중치 값을 제한하기 위해 매우 간단한 클리핑을 적용합니다.
즉, discriminator의 가중치는 hyperparameter $c$에 의해 제어되는 특정 범위 내에 있어야합니다.

WGAN에 대한 두 가지 중요한 기여는 다음과 같습니다.
- 실험에서 mode collapse의 징후가 없으며 generator는 critic이 잘 수행 할 때 여전히 학습 할 수 있습니다.
아래와 같이 DCGAN에서 배치 정규화를 제거하더라도 WGAN은 계속 수행 할 수 있습니다.
WGAN - Issues
Clipping을 통해 critic의 모델에 Lipschitz 제약 조건을 적용하여 Wasserstein 거리를 계산할 수 있습니다.

연구 논문 인용 : Weight clipping은 Lipschitz constraint을 적용하는 분명히 끔찍한 방법입니다. 클리핑 매개 변수가 크면 weight가 한계에 도달하는 데 오랜 시간이 걸리므로 critic를 최적 상태로 훈련하기가 더 어려워집니다. clipping이 작으면 레이어 수가 많거나 batch normalization을 사용하지 않을 때 (예 : RNN) 쉽게 gradient가 사라지게 될 수 있습니다. ... 그리고 단순성과 이미 좋은 성능으로 인해 가중치 클리핑을 고수했습니다.
WGAN의 어려움은 Lipschitz constraint 을 적용하는 것입니다.
클리핑은 간단하지만 몇 가지 문제가 있습니다.
모델은 여전히 저품질 이미지를 생성할 수 있으며 특히 하이퍼 파라미터 $c$가 올바르게 조정되지 않은 경우 수렴되지 않습니다.

모델 성능은이 하이퍼 파라미터에 매우 민감합니다.
아래 다이어그램에서 batch normalization이 꺼져있는 경우 c가 0.01에서 0.1로 증가하면 discriminator가 vanishing하는 그라데이션에서 exploding하는 그라데이션으로 이동합니다.
Model capacity
weight clipping은 weight regulation으로 작동합니다.
모델 f의 capacity을 줄이고 복잡한 기능을 모델링하는 기능을 제한합니다.
아래 실험에서 첫 번째 행은 WGAN에서 추정한 값 함수의 윤곽 플롯입니다.
두 번째 행은 WGAN-GP라는 WGAN의 변형에 의해 추정됩니다.
WGAN의 감소된 capacity는 개선된 WGAN-GP가 할 수있는 반면 모델의 모드 (주황색 점)를 둘러싸는 복잡한 경계를 생성하지 못합니다.

Wasserstein GAN with gradient penalty (WGAN-GP)
WGAN-GP는 weight clipping 대신 gradient penalty를 사용하여 Lipschitz 제약 조건을 적용합니다.
Gradient penalty
미분 할 수 있는 함수 f는 모든 곳에서 norm이 최대 1인 기울기가있는 경우에만 1-Lipschitz입니다.
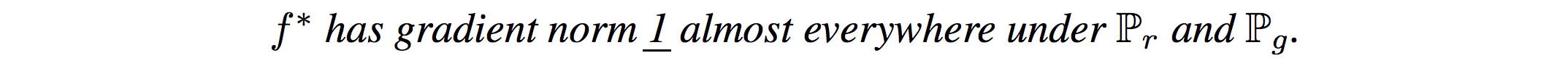
'딥러닝관련' 카테고리의 다른 글
| 배치(batch) 처리의 이점 (0) | 2021.05.12 |
|---|---|
| 신경망 정리 2 (선형 함수, 비선형 함수, ReLU, Softmax, 행렬 계산...) (3) | 2021.05.02 |
| CAM 및 Grad-CAM 정리 (0) | 2021.01.29 |
| DeblurGAN: Blind Motion Deblurring Using Conditional Adversarial Networks 논문 리뷰 (0) | 2021.01.18 |

