better-tomorrow.tistory.com/entry/%EC%8B%A0%EA%B2%BD%EB%A7%9D
신경망 정리 1
better-tomorrow.tistory.com/entry/Perceptron-%ED%8D%BC%EC%85%89%ED%8A%B8%EB%A1%A0 Perceptron (퍼셉트론) 퍼셉트론 정의 퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력 퍼셉트론의 신호는 흐른..
better-tomorrow.tistory.com
위 내용에 이어서...
비선형 함수
계단 함수와 시그모이드 함수의 공통점은 모두 비선형 함수라는 것
그렇다면 비선형 함수란?
'선형이 아닌 함수' : 직선 1개로는 그릴 수 없는 함수
신경망에서는 활성화 함수로 비선형 함수를 사용해야 한다.
선형 함수를 이용하면 신경망의 층을 깊게 하는 의미가 없어지기 때문
선형 함수의 문제는 층을 아무리 깊게 해도 '은닉층이 없는 네트워크'로도 똑같은 기능을 할 수 있다.
선형 함수 h(x) = cx를 활성화 함수로 사용한 3층 네트워크가 있다고 가정
y(x) = h(h(h(x)))가 된다.
이 계산은 y(x) = c * c * c * x 처럼 세번의 곱셈을 구행하지만 실은 y(x) = ax와 똑같은 식
즉 은닉층이 없다고 봐도 된다.
그래서 층을 쌓는 혜택을 얻고 싶다면 활성화 함수로는 비선형 함수를 사용해야 함.
(막간으로 선형과 비선형 함수를 아래를 참조해서 조금 더 정리하자면)
study.com/academy/lesson/nonlinear-function-definition-examples.html
Nonlinear Function: Definition & Examples - Video & Lesson Transcript | Study.com
In this lesson, we will familiarize ourselves with linear functions in order to define and understand what nonlinear functions are. We will become...
study.com
비선형 함수 (nonlinear function)
- 선형 함수가 아닌 함수
- 비선형 함수의 그래프는 선이 아님.
- 점 사이에 변화하는 기울기를 갖음
- 선형 함수에서 가장 높은 지수가 1인 다항식 또는 수평선으로 정의하지만, 비선형 함수는 그 외 다른 모든 함수
- y = x ^ 2 함수는 지수가 2이며 점 사이의 기울기가 다르기 때문에 비선형 함수다.
ReLU 함수
Rectified Linear Unit 함수
입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하면 0을 출력하는 함수
구현
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return np.maximum(0, x)
x = np.arange(-5.0 , 5.0 , 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-1, 6)
plt.show()
행렬의 내적 곱
예시
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print(np.dot(A, B))결과
[[19 22]
[43 50]]

두 행렬의 내적을 np.dot()으로 계산 가능하다.
신경망의 내적
넘파이로 신경망 구현
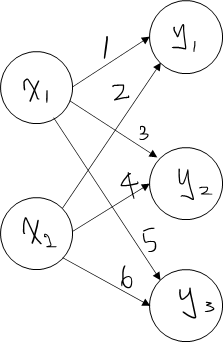
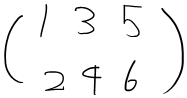
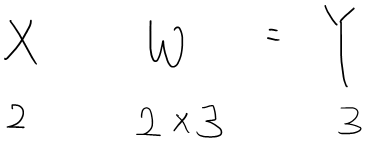
파이썬으로 위 신경망 구현
import numpy as np
X = np.array([1, 2])
print("X.shape : ", X.shape)
W = np.array([[1, 3, 5],[2, 4, 6]])
print("W :" , W)
print("W.shape", W.shape)
Y = np.dot(X, W)
print("np.dot(X, W) : ", Y)결과
X.shape : (2,)
W : [[1 3 5]
[2 4 6]]
W.shape (2, 3)
np.dot(X, W) : [ 5 11 17]
3층 신경망 구현
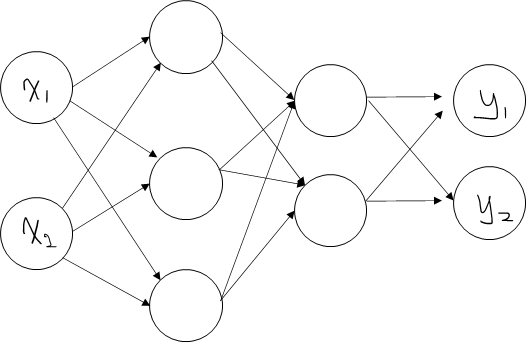

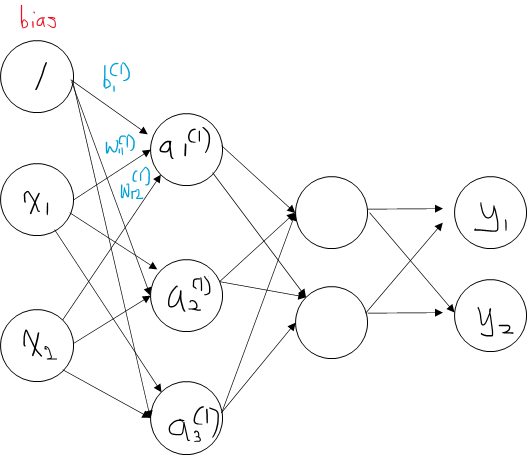
1층의 첫 번째 뉴런에 대해서 수식을 아래와 같이 계산할 수 있다.
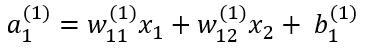
여기에서 행렬의 내적을 이용하면 1층의 가중치 부분을 간소화 할 수 있다.
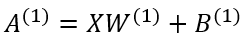
이를 다시 풀어보면
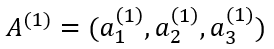
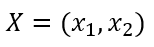
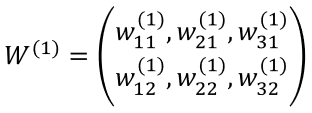
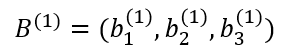
위 내용을 넘파이 배열을 이용하여 구현
import numpy as np
X = np.array([1, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.5])
print("W1.shape", W1.shape)
print("X.shape", X.shape)
print("B1.shape", B1.shape)
A1 = np.dot(X, W1) + B1
print(A1)결과
W1.shape (2, 3)
X.shape (2,)
B1.shape (3,)
[0.3 0.7 1.3]여기서 신경망 특성을 위해 활성화 함수 sigmoid를 추가한다.
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
X = np.array([1, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.5])
print("W1.shape", W1.shape)
print("X.shape", X.shape)
print("B1.shape", B1.shape)
A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1)
print("A1 : ", A1)
print("Z1 : ", Z1)W1.shape (2, 3)
X.shape (2,)
B1.shape (3,)
A1 : [0.3 0.7 1.3]
Z1 : [0.57444252 0.66818777 0.78583498]
이어서 1층에서 2층으로 가는 신경망 구현 (bias 추가)
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
X = np.array([1, 0.5])
print("=============== 첫 번째 층 =======================")
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.5])
print("W1.shape", W1.shape)
print("X.shape", X.shape)
print("B1.shape", B1.shape)
A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1)
print("A1 : ", A1)
print("Z1 : ", Z1)
print("=============== 두 번째 층 =======================")
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
print("Z1.shape", Z1.shape)
print("W2.shape", W2.shape)
print("B2.shape", B2.shape)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)
print("A2 : ", A2)
print("Z2 : ", Z2)
결과
=============== 첫 번째 층 =======================
W1.shape (2, 3)
X.shape (2,)
B1.shape (3,)
A1 : [0.3 0.7 1.3]
Z1 : [0.57444252 0.66818777 0.78583498]
=============== 두 번째 층 =======================
Z1.shape (3,)
W2.shape (3, 2)
B2.shape (2,)
A2 : [0.5268323 1.23537188]
Z2 : [0.62874399 0.7747574 ]
이어서 2층에서 출력층으로 가는 신경망 구현 (bias 추가) -> 활성화 함수에서 항등 함수로 사용 -> 입력을 그대로 출력
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
X = np.array([1, 0.5])
print("=============== 첫 번째 층 =======================")
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.5])
print("W1.shape", W1.shape)
print("X.shape", X.shape)
print("B1.shape", B1.shape)
A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1)
print("A1 : ", A1)
print("Z1 : ", Z1)
print("=============== 두 번째 층 =======================")
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
print("Z1.shape", Z1.shape)
print("W2.shape", W2.shape)
print("B2.shape", B2.shape)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)
print("A2 : ", A2)
print("Z2 : ", Z2)
print("=============== 출력 층 =======================")
def identity_function(x):
return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
print("Z2.shape", Z2.shape)
print("W3.shape", W3.shape)
print("B3.shape", B3.shape)
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)
print("A3 : ", A3)
print("Y : ", Y)
출력
=============== 첫 번째 층 =======================
W1.shape (2, 3)
X.shape (2,)
B1.shape (3,)
A1 : [0.3 0.7 1.3]
Z1 : [0.57444252 0.66818777 0.78583498]
=============== 두 번째 층 =======================
Z1.shape (3,)
W2.shape (3, 2)
B2.shape (2,)
A2 : [0.5268323 1.23537188]
Z2 : [0.62874399 0.7747574 ]
=============== 출력 층 =======================
Z2.shape (2,)
W3.shape (2, 2)
B3.shape (2,)
A3 : [0.31782588 0.69852616]
Y : [0.31782588 0.69852616]
이를 조금 더 보기 좋게 정리
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def identity_function(x):
return x
def init_network():
network = {}
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.5])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])
return network
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)
return y
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)출력
[0.31782588 0.69852616]출력층 설계하기
신경망은 분류와 회귀에 모두 이용될 수 있다.
그러나 일반적으로 회귀에는 항당 함수를, 분류에는 소프트맥스 함수를 사용한다.
항등 함수와 소프트맥스 함수 구현하기
항등함수는 입력을 그대로 출력.
출력층에서 항등 함수를 사용하면 입력 신호가 그대로 출력 신호가 된다.
분류에 사용하는 소프트맥스 함수(softmax function)의 식
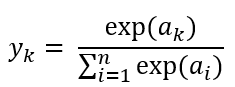

softmax 함수를 그림으로 표현한다면 아래와 같다.
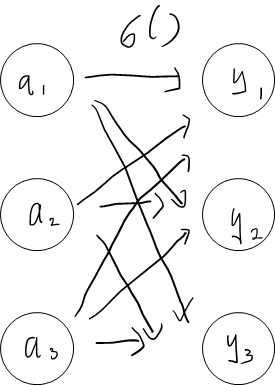
파이썬으로 구현해보자
"""
softmax
"""
import numpy as np
a = np.array([0.3, 2.9, 4.0])
exp_a = np.exp(a) # 지수 함수
print(exp_a)
sum_exp_a = np.sum(exp_a)
print(sum_exp_a)
y = exp_a / sum_exp_a
print(y)결과
[ 1.34985881 18.17414537 54.59815003]
74.1221542101633
[0.01821127 0.24519181 0.73659691]
소프트맥스 함수 구현 시 주의점
위의 softmax 함수는 식을 제대로 표현하지만 실제 컴퓨터로 계산할 때는 결함이 있다.
오버플로 문제
소프트맥스 함수는 지수 함수를 사용하는데, 당연히 지수 함수는 쉽게 아주 큰 값을 내뱉는다.
(e^10 : 20,000, e^100: 0이 40개 넘는 숫자, e^1000 : 무한대 inf)
이런 큰 값끼리 나눗셈을 하면 결과 수치가 '불안정' 해짐
[컴퓨터는 크기가 유한한 데이터로 다룸. 표현할 수 있는 수의 범위가 한정되어 너무 큰 값은 표현할 수 없다는 문제가 발생, 이를 오버플로라고 함]
위 문제를 해결하기 위해 소프트맥수 함수를 개선
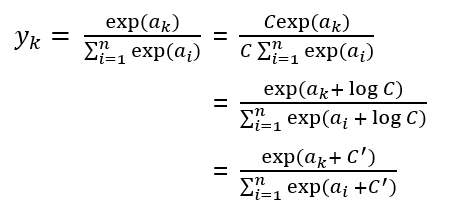
1) C라는 임의의 정수를 분자와 분모 양쪽에 곱함
2) C를 지수 함수 exp() 안으로 옮겨 logC로 만듦
3) logC를 C'의 새로운 기호로 바꾼다.
C'에 어떤 값을 대입해도 상관없다. 결과는 바뀌지 않는다. 오버플로를 막을 목적으로 보통, 입력 신호 중 최대값을 이용한다.
예시
"""
fixed softmax
"""
import numpy as np
a = np.array([1010, 1000, 990])
print(np.exp(a) / np.sum(np.exp(a))) # 소프트 맥스 계산
c = np.max(a)
print(a - c)
print(np.exp(a - c) / np.sum(np.exp(a-c))) # 수정된 소프트 맥스 계산결과
RuntimeWarning: overflow encountered in exp
print(np.exp(a) / np.sum(np.exp(a))) # 소프트 맥스 계산
RuntimeWarning: invalid value encountered in true_divide
print(np.exp(a) / np.sum(np.exp(a))) # 소프트 맥스 계산
[nan nan nan]
[ 0 -10 -20]
[9.99954600e-01 4.53978686e-05 2.06106005e-09]
소프트맥스 함수의 특징
- 소프트맥스 함수를 사용하면 신경망의 출력이 0에서 1사이의 실수가 된다.
- 소프트맥스 함수의 총합은 1이다.
- 이것이 소프트맥스 함수의 중요한 성질
- 소프트맥스 함수의 출력을 '확률'로 해석할 수 있음
- 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않는다.
- 지수 함수 y = exp(x)가 단조 증가 함수이기 때문
- 신경망 분류에서는 일반적으로 가장 큰 출력을 내는 뉴런에 해당하는 클래스로만 인식
- 소프트맥스 함수를 적용해도 출력이 가장 큰 뉴런의 위치가 달라지지 않기 때문에, 분류할 때 출력층에서 생략해도 됨
출력층의 뉴런 수 정하기
출력층의 뉴런 수는 풀려는 문제에 맞게 적절히 정해야 한다.
분류에서는 분류하고 싶은 클래스 수로 설정하는 것이 일반적
내용 참고
book.naver.com/bookdb/book_detail.nhn?bid=11492334
밑바닥부터 시작하는 딥러닝
직접 구현하고 움직여보며 익히는 가장 쉬운 딥러닝 입문서!『밑바닥부터 시작하는 딥러닝』은 라이브러리나 프레임워크에 의존하지 않고, 딥러닝의 핵심을 ‘밑바닥부터’ 직접 만들어보며
book.naver.com
'딥러닝관련' 카테고리의 다른 글
| 배치(batch) 처리의 이점 (0) | 2021.05.12 |
|---|---|
| CAM 및 Grad-CAM 정리 (0) | 2021.01.29 |
| GAN — Wasserstein GAN & WGAN-GP (0) | 2021.01.18 |
| DeblurGAN: Blind Motion Deblurring Using Conditional Adversarial Networks 논문 리뷰 (0) | 2021.01.18 |

