이전까지는 가중치 매개변수에 대한 손실 함수의 기울기는 수치 미분을 사용해 구현
수치 미분은 단순하고 구현하기도 쉽지만 계산이 오래 걸린다는 게 단점.
가중치 매개변수의 기울기를 효율적으로 계산하는 '오차역전파(back propagation)'이 있음
back propagation의 계산 과정을 그래프로 나타낼 수 있으며 이를 계산 그래프(computational graph)라고 표현
노드(node)와 엣지(edge)로 표현된다.
1. 계산 그래프로 풀기
ex)
슈퍼에서 1개에 100원인 사과 2개 구매. 이때 지불 금액 계산, 단 소비세가 10% 부과
아래와 같이 표현 가능

계산 그래프에 의해 220원을 지불한다는 사실을 안다.
위 그래프에서 연산만 노드안에 표기하고, 개수와 세율을 밖으료 표기해본다.

두 번째 문제
슈퍼에서 1개에 100원인 사과 2개, 150원인 귤 3개 구매. 이때 지불 금액 계산, 단 소비세가 10% 부과

계산 그래프는 왼쪽에서 오른쪽으로 계산을 진행한다.
왼쪽에서 오른쪽으로 계산을 진행하는 단계를 순전파 forward propagation이라하고
오른쪽에서 왼쪽으로 계산을 진행하는 단계를 역전파 backward propagation이라고 한다.
2. 국소적 계산
계산 그래프의 특징은 '국소적 계산'을 전파함으로써 최종 결과를 얻는다는 점에 있다.
(국소적 : '자신과 직접 관계된 작은 범위')
국소적 계산은 결국 전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만으로 다음 결과를 출력할 수 있다는 것.
각 노드는 자신과 관련된 계산 외에는 아무것도 신경 쓸 게 없다.
이처럼 계산 그래프는 국소적 계산에 집중한다.
3. 왜 계산 그래프로 푸는가
계산 그래프의 이점
1. 국소적 계산
전체가 아무리 복잡해도 각 노드에서는 단순한 계산에 집중하여 문제를 단순화할 수 있다.
2. 중간 계산 결과를 모두 보관 가능
3. 역전파를 통해 '미분'을 효율적으로 계산할 수 있는 점
문제 1을 다시 봐보자

위는 사과 3개 사서 소비세를 포함한 최종 금액을 구하는 것,
만약 사과 가격이 오르면 최종 금액에 어떤 영향을 끼치는 지를 알고 싶다고 하면...
이는 '사과 가격에 대한 지불 금액의 미분'을 구하는 문제에 해당
사과 값을 x, 지불 금액을 L이라 했을 때 아래의 식을 구하는 것

이는 사과의 값이 '아주 조금' 올랐을 때 지불 금액이 얼마나 증가하느냐를 알 수 있음
결과만 보면
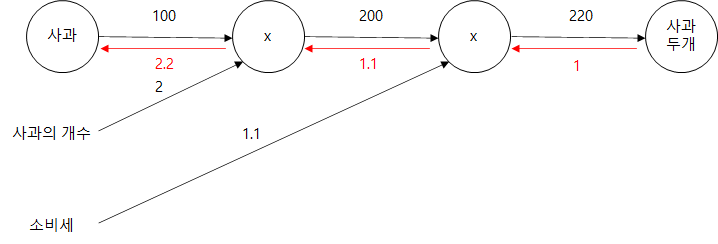
이 전파는 '국소적 미분'을 전달한다.
'1 → 1.1 → 2.2' 순으로 미분 값 전달.
이 결과로 부터 '사과 가격에 대한 지불 금액의 미분' 값은 2.2라 할 수 있음.
사과가 1원 오르면 최종 금액은 2.2원 오른다.
(정확히는 사과 값이 아주 조금 오르면 최종 금액은 그 아주 작은 값의 2.2배만큼 오른다)
사과 뿐만 아니라 사과의 개수나, 소비세에 대한 금액의 미분도 계산할 수 있다.
계산 그래프의 이점은 순전파와 역전파를 활용해서 각 변수의 미분을 효율적으로 구할 수 있다는 것.
내용 참고
book.naver.com/bookdb/book_detail.nhn?bid=11492334
밑바닥부터 시작하는 딥러닝
직접 구현하고 움직여보며 익히는 가장 쉬운 딥러닝 입문서!『밑바닥부터 시작하는 딥러닝』은 라이브러리나 프레임워크에 의존하지 않고, 딥러닝의 핵심을 ‘밑바닥부터’ 직접 만들어보며
book.naver.com
'딥러닝관련 > 기초 이론' 카테고리의 다른 글
| 특이값 분해 (singular decomposition) (0) | 2021.06.04 |
|---|---|
| 신경망 정리 9 (연쇄 법칙 chain rule) (0) | 2021.05.30 |
| 신경망 정리 7 (학습 알고리즘 구현) (0) | 2021.05.29 |
| 기초 행렬 이론 정리 (0) | 2021.05.27 |
| 신경망 정리 6 (경사법, 경사 하강법) (0) | 2021.05.24 |


