정렬
1. 선택 정렬
처리되지 않은 데이터 중에서 [가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸는 것을 반복]
이중 반복문을 통해 구현
선형 시간 소요
N번 만큼 가장 작은 수를 찾아서 맨 앞으로 보내야 한다.
시간 복잡도 O(N^2)
과정

처리되지 않은 데이터 중 가장 작은 0을 선택해 가장 앞자리 7과 바꿈

처리되지 않은 데이터 중 가장 작은 1을 선택해 가장 앞자리 5과 바꿈

처리되지 않은 데이터 중 가장 작은 2을 선택해 가장 앞자리 9과 바꿈

이 과정을 반복하면

C++ 코드
#include <iostream>
using namespace std;
int main(void)
{
int n = 10;
int arr[10] = { 7, 5, 9, 0, 3, 1, 6, 2, 4, 8 };
for (int i = 0; i < n; i++)
{
// swap을 위한 가장 작은 인덱스 변수 선언
int min_index = i;
// i 기준 다음 index부터 탐색
for (int j = i + 1; j < n; j++)
{
// min index에 있는 값보다 현재 탐색 값이 더 작으면 min_index를 갱신
if (arr[j] < arr[min_index])
min_index = j;
}
// 배열 바꾸기
swap(arr[i], arr[min_index]);
}
for (int i = 0; i < n; i++) {
cout << arr[i] << ' ';
}
}
2. 삽입 정렬
처리되지 않은 데이터를 하나씩 골라 적절한 위치에 삽입
구현 난이도는 높지만 선택 정렬보다 빠르게 동작
삽입 정렬은 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 매우 빠르게 동작
이중 반복문이 중첩되어 사용
시간 복잡도 O(N^2)


9와 7을 비교해서 크면 그대로 유지

현재 기준 왼쪽 데이터들과 비교해본다.

이런식으로 비교
/*
선택정렬은 느림
"데이터를 하나씩 확인하며, 각 데이터를 적절한 위치에 삽입?"
-> 삽입 정렬
선택 정렬에 비해 실행 시간 측면에서 더 효율적인 알고리즘
선택 정렬 : 모든 원소를 비교
삽입 정렬 : 필요한 원소만 비교
삽입 정렬 : 특정한 데이터가 적절한 위치에 들어가기 이전에, 그 앞까지의 데이터는 이미 정렬되어 있다고 가정.
두 번째 데이터부터 시작, 첫 번째 데이터는 그 자체로 정렬되어 있다고 판단.
시간복잡도 O(N 제곱)
현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 빠르게 동작
*/
#include <iostream>
using namespace std;
int n = 10;
int arr[10] = { 7, 5, 9, 0, 3, 1, 6, 2, 4, 8 };
int main(void) {
for (int i = 1; i < n; i++) {
// 인덱스 i부터 1까지 감소하며 반복하는 문법
for (int j = i; j > 0; j--) { // j는 삽입하고자 하는 위치
// 한 칸씩 왼쪽으로 이동
if (arr[j] < arr[j - 1]) {
swap(arr[j], arr[j - 1]);
}
// 자기보다 작은 데이터를 만나면 그 위치에서 멈춤
else break;
}
}
for (int i = 0; i < n; i++) {
cout << arr[i] << ' ';
}
}
3. 퀵 정렬
기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법
일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘 중 하나
첫 번째 데이터를 기준 데이터로(pivot)로 설정
퀵 정렬은 평균의 경우 O(NlogN)의 시간 복잡도를 가진다.
최악의 경우 O(N^2)
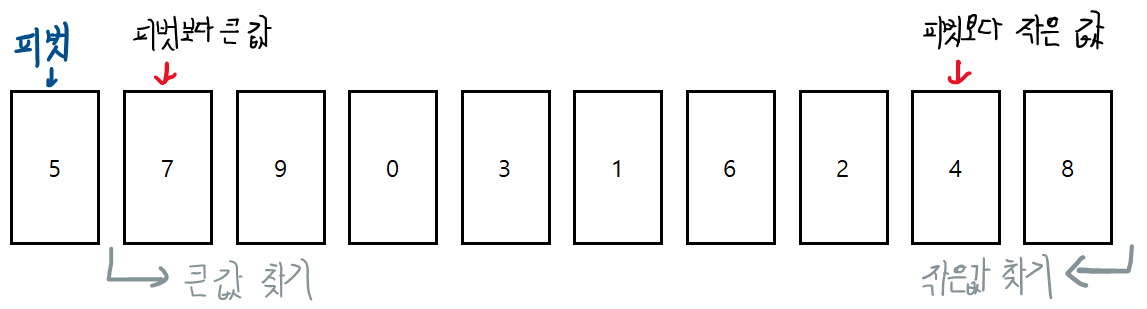

.... 반복
계속 바꾸다 보면 아래와 같이 위치가 엇갈리는 경우,
피벗과 작은 데이터의 위치를 서로 변경

아래와 같이 위치를 교체하면 피벗을 기준으로 왼쪽 데이터들은 5보다 작고, 오른쪽 데이터들은 5보다 크다는 특징이 있다.
이렇게 피벗을 기준으로 데이터 묶음을 나누는 작업을 분할.

이렇게 나눈 후 나눈 영역에 대해서도 아래와 같이 퀵 정렬을 수행한다.

퀵 정렬이 빠른이유..
분할이 절반씩 일어난다면 전체 연산 횟수로 O(NlogN)(밑2) 을 기대할 수 있음
/*
기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾸는 방법
일반적인 상황에서 가장 많이 사용되는 정렬 알고리즘
병합 정렬과 더불어 프로그래밍 언어의 정렬 라이브러리의 근간이 되는 알고리즘
퀵 정렬, 첫 번쨰 데이터를 기준 데이터(pivot)로 설정
평균 Nlog(N)
최악 O(N제곱)
*/
#include <iostream>
using namespace std;
int n = 10;
int arr[10] = { 5, 7, 9, 0, 3, 1, 6, 2, 4, 8 };
void quickSort(int* arr, int start, int end) {
if (start >= end) return; // 원소가 1개인 경우 종료
int pivot = start; // 피벗은 첫 번째 원소
int left = start + 1;
int right = end;
// 엇갈릴 때까지 반복
while (left <= right) {
// 피벗(arr[pivot])보다 큰 데이터(arr[left])를 찾을 때까지 반복 -> 찾으면 조건문이 false가 되어 탈출
while (left <= end && arr[left] <= arr[pivot])
left++;
// 피벗(arr[pivot])보다 작은 데이터(arr[right])를 찾을 때까지 반복 -> 찾으면 조건문이 fasle가 되어 탈출
while (right > start && arr[right] >= arr[pivot])
right--;
// 엇갈렸다면 작은 데이터와 피벗을 교체
if (left > right)
swap(arr[pivot], arr[right]);
// 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
else
swap(arr[left], arr[right]);
}
// 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
quickSort(arr, start, right - 1);
quickSort(arr, right + 1, end);
}
int main(void) {
quickSort(arr, 0, n - 1);
for (int i = 0; i < n; i++) {
cout << arr[i] << ' ';
}
}4. 계수 정렬
특정한 조건이 부합할 때만 사용할 수 있지만 매우 빠르게 동작하는 정렬 알고리즘
데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 사용 가능
데이터의 개수가 N, 데이터 (양수) 중 최대값이 K일 때 최악의 경우에도 수행 시간 O(N+K)를 보장
인덱스에 따른 개수(count)를 기록하고 인덱스를 개수 만큼 표현함으로써 정렬
때에 따라서 심각한 비효율성 초래 - 0과 999,999로 단 2개만 존재하는 경우
동일한 값을 가지는 데이터가 여러 개 등장할 때 효과적으로 사용 가능
#include <iostream>
#define MAX_VALUE 9
using namespace std;
int n = 15;
// 모든 원소의 값이 0보다 크거나 같다고 가정
int arr[15] = { 7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2 };
// 모든 범위를 포함하는 배열 선언(모든 값은 0으로 초기화)
int cnt[MAX_VALUE + 1];
int main(void) {
// O(N)
for (int i = 0; i < n; i++) {
cnt[arr[i]] += 1; // 각 데이터에 해당하는 인덱스의 값 증가
}
// O(K)
for (int i = 0; i <= MAX_VALUE; i++) { // 배열에 기록된 정렬 정보 확인
for (int j = 0; j < cnt[i]; j++) {
cout << i << ' '; // 띄어쓰기를 기준으로 등장한 횟수만큼 인덱스 출력
}
}
}
내용 및 코드 참고
www.youtube.com/watch?v=KGyK-pNvWos&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=4
'알고리즘 > 이론' 카테고리의 다른 글
| 다이나믹 프로그래밍(Dynamic Programming) (0) | 2021.04.13 |
|---|---|
| 이진 탐색 (binary search) 알고리즘 (0) | 2021.04.13 |
| 재귀(recursive) 함수 (0) | 2021.04.12 |
| queue 자료구조 설명 및 구현(c++) (0) | 2021.04.09 |
| DFS & BFS 이해하기 및 구현(C++) (9) | 2021.03.08 |



