Neural Architecture Search with Reinforcement Learning. part.1 (논문 리뷰)
논문 : https://arxiv.org/pdf/2005.11074.pdf
Neural architecture search 분야에 관심이 생겨 관련 분야의 첫 논문을 시작으로 정리를 해보고자 한다.
Abstract
Neural network는 이미지, 소리, 그리고 자연어를 이해와 같은 많은 어려운 학습 task에서 강력하고 유연한 모델이다.
그러나 neural network를 디자인하기란 여전히 어렵다
(실제로 그렇다, 내 데이터에 적합한 모델을 찾기에는 많은 시간과 노력이 필요하다.
ex, 논문 분석 -> 코드 구현 -> 학습 -> 테스트 -> 결과 분석 -> 좋은 결과가 나올 때까지 반복...)
본 논문에서는 RNN을 사용해 neural network model descriptions를 생성하고, 그 RNN을 강화학습과 함께 생성된 네트워크가 validation set에섯 기대하는 accuracy를 최대화 하는 방향으로 학습을 진행함.
CIFAR-10 : 3.65% test error rate (비슷한 구조를 사용했던 이전의 최신 모델보다 0.09% 나은 성능 및 1.05배 빠름)
Peen Treebank : 새로운 recurrent cell 생성 (널리 사용되는 LSTM cell 및 다른 최신 baseline보다 더 좋은 결과를 보임)
Introduction
Deep neural network는 최근 몇년 동안 speech recognition, image recognition, machine translation과 같은 분야에서 많은 성공을 거두었음
이러한 성공과 함께에는 paradigm shift가 있었다. (feature designing -> architecture designing)
(우리가 딥러닝을 하는데 직접 사람이 feature engineering을 하지는 않으니)
이에 feature design은 쉬워졌지만, architecture를 디자인 하는데는 여전히 많은 전문적 지식과 함께 많은 시간 또한 요구된다.
이에 이 논문에서는 Neural Architecture Search를 제안한다.(gradient-based method for finding good architecture)

이 논문에서는 신경망의 structure와 connectivity가 일반적으로 variable-length string으로 지정될 수 있다는 관찰을 기반
(전체적인 구조가 문자열 형태로 정의할 수 있다는 걸 의미하는 것 같음 ex, layer2 : ["dilated convolution"] -> 좀더 살펴보자)
따라서 recurrent neural network(the controller)로 이러한 string을 생성하는 것이 가능함.
Real data에 대해 string으로 지정된 네트워크("child network")를 training하면 validation set의 accuracy가 나온다.
이 validation set의 accuracy를 reward signal($R$)로 하여 , policy gradient를 계산하여 controller를 update할 수 있다.
결과적으로 다음 iteration에서 controller는 높은 accuracies를 받는 arcitecture에 높은 확률을 줄 것이다.
잠시 정리해보면 아래의 흐름대로 진행되는 거 같다.
1. RNN-controller가 모델 구조를 만들고
2. 생성된 구조(child network)가 real data에 대해 training을 하고
3. 생성된 구조(child network)에서 validation set에 대한 accuracy를 측정하고
4. 이 accuracy를 강화학습에서 쓰이는 reward로 여겨
5. 이 reward에 따라 controller가 높은 reward를 같은 architecture를 생성하도록 학습한다.
이 실험은 Neural Architecture Search가 처음부터 좋은 모델을 설계할 수 있음을 보여준다.
Methods
1. Recurrent Neural Netweork를 사용하여 convolutional architecture를 생성하는 방법을 소개
2. Sampling된 architectures의 expected accuracy를 최대화하기 위해 policy gradient method 방법으로 RNN 학습 방법 소개
3. core approach의 몇 가지 개선 사항을 소개(e.g skip connections, parameter server)
4. Recurrent architectures 생성에 초점을 맞춰 진행
1) Generate Model Descriptions with a Controller Recurrent Neural Network
- Neural Architecture Search(NAS) 에서는 controller를 사용하여 neural networks의 architecture hyper-parameter 생성
- 유연성을 위해, controller는 recurrent neural network로 구현
- 만약 convolutional layer들만 있는 neural network를 predict하고 싶다고 가정.
- 아래와 같이 controller로 hyper-paramet token sequence 생성할 수 있음.

- 실험에서 number of layers가 특정 값을 넘어가면 architecture generating process가 중단된다.
- 이 특정 값은 training이 진행됨에 따라 증가하는 schedule을 가짐
- Controller RNN이 architecture 생성을 마치면 이 architecture로 neural network가 build되고 training된다.
- 수렴되는 지점에서, hold-out validation에 대한 network의 accuracy가 기록된다.
- Controller RNN의 parameter $θ_{c}$는 proposed architecture의 expected validation acccuracy를 maximize하기 위해 최적화됨
2) Training with Reinforce
Controller가 predict하는 list of tokens는 child network의 architecture를 디자인 하기 위한 $a_{1:T}$ list of action로 볼 수 있다. 수렴 지점에서, 이 child network는 held-out dataset에서 accuracy $R$을 달성해야 한다. 이 accuracy $R$을 reward signal로 사용하고 강화학습을 사용하여 controller를 훈련할 수 있다. 최적의 architecture를 찾기 위해 expected reward $J(θ_{c})$ 가 최대화하도록 controller에 요청
$J(θ_{c}) = E_{P(a_{1:T};θ_{c})}[R]$
Reward signal $R$ 은 미분 불가능(non-differentiable) 하므로, 반복적으로 업데이트 하기 위해 policy gradient method를 사용해야 함. 이 논문에서는 아래의 Willams(1992)의 reinforce rule을 적용함

위의 empirical approximation은 아래와 같이 나타낼 수 있다고 함
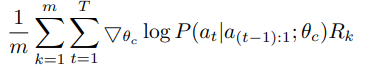
$m$ : controller가 한 배치에서 샘플링하는 서로 다른 architecture 수
$T$ : controller가 neural network architecture를 디자인하기 위해 예측해야 하는 hyper-parameter 수
$R_{k}$ : $k$번째 neural network architecture가 training dataset에서 trained 후 달성하는 validation accuracy
위 업데이트는 gradient에 대한 unbiased 추정치이지만, high variance를 가진다.
이 high variance를 줄이기 위해 baseline function을 사용한다.
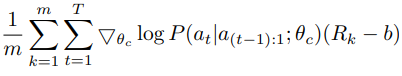
$b$ : 이전 architecture 정확도의 exponential moving average.
($b$가 current action에 의존하지 않는 한 위 수식은 여전히 unbiased gradient 추정치이다)
Accelerate Training with Parallelism and Asynchronous Updates
- Controller parameters $θ_{c}$에 대한 각 gradient update는 하나의 child network를 convergence으로 training하는 것에 해당.
- Child network를 training 하는 데 시간이 꽤 걸리므로, controller의 training process speed를 높이기 위해
distributed training과 asynchronous parameter update를 사용.
- $S$ shards의 parameter-server가 있는 parameter-server scheme을 사용
-> $K$ controller replicas에 대한 shared parameters를 저장하기 위해
- 각 controller replicas는 parallel로 trained된 m개의 서로 다른 child architectures를 샘플링한다.
- 이후 controller는 convergence 시 m architectures의 mini-batch 결과에 따라 gradient를 수집하고 모든 controller replicas에서 weight update를 위해 parameter server로 보낸다.
- 구현적인 측면에서, 각 child network의 convergence는, training이 특정 epoch 수를 초과할 때 도달한다.
위 내용은 아래의 figure 참고
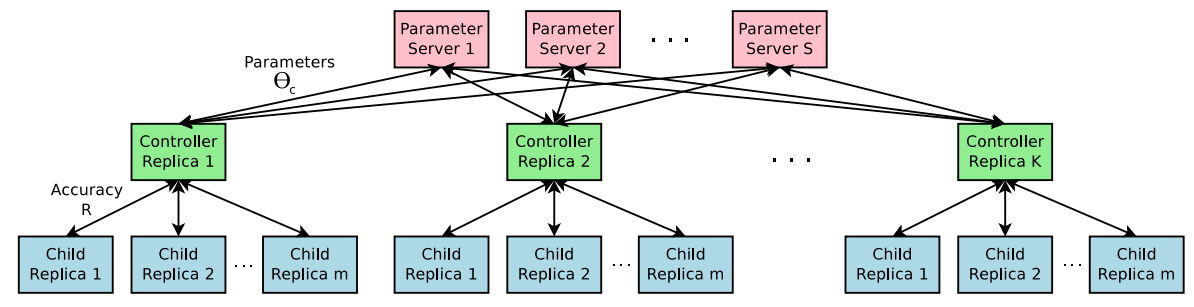
3) Increase Architecture Complexity with Skip connections and Other Layer Types
이제까지 정리한 내용에 따르면 GoogleNet이나 ResNet에서 사용하는 것과 같은 branching layers나 skip connections과 같은 것들이 없다. Controller가 이러한 connections를 예측할 수 있도록 하기 위해 attention mechanism을 기반으로 구축된 set-selection type attention을 사용. Layer N에서, connection이 필요한 previous layer를 가리키기 위해 N-1개의 content-based sigmoid가 있는 anchor point를 추가.
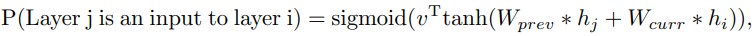
$h_{j}$ : $j$번째 layer에 대한 anchor point에서 controller의 hidden state를 나타내며, 여기서 $j$는 N - 1까지의 범위. 그런 다음 이 sigmoid에서 sampling하여 현재 layer에 대한 입력으로 사용할 이전 layer를 결정. 행렬 $W_{prev}$, $W_{curr}$과 $v$는 trainable parameters.
- 이러한 connections도 probability distribution으로 정의되므로, reinforce 방법은 significant modifications 없기 계속 적용 가능
아래 이미지는 controller가 현재 layer에 대한 입력으로 원하는 layer를 결정하기 위해 skip connections를 사용하는 방법
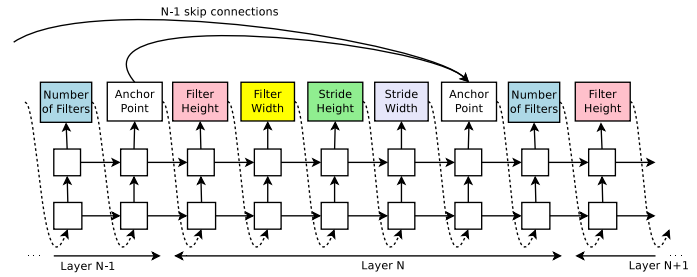
프레임워크에서 한 layer에 많은 입력 layer가 있으면 모든 입력 layers는 depth dimension으로 concatenate된다. 이 경우 한 layer가 다른 layer와 호환되지 않거나 한 layer에 다른 입력 또는 출력이 있을 수 없는 "compilation failures"를 유발할 수 있다.
이러한 문제들을 해결하기 위해 세 가지 간단한 기술을 사용.
첫째, layer가 어떠한 input layer에도 연결되어 있지 않으면, 이미지가 input layer로 사용됨.
둘째, final layer에서 connected 되지 않은 모든 layer의 ouputs을 가져와 최종 hiddenstate를 최종 classifier로 보내기 전에 concatenate.
마지막으로, 연결한 input layers의 크기가 다른 경우 연결된 layer의 크기가 같도록 small layers를 0으로 padding 한다.
이제까지 architecture가 learning rate를 predict하지 않고 convolutional layer로만 구성되어 있다고 가정하였다.
-> 제한적임
predictions 중 하나에 learning rate를 추가하는 것이 가능.
또한 pooling, local contrast normalization, batchnorm 등을 predict 하는 것도 가능.
더 많은 types의 layer를 추가할 수 있으려면,
- controller RNN에 layer type을 예측하는 additional step을 추가한다음.
- 이와 관련한 hyper-parameter를 추가
4) Generate Recurrent Cell Architectures
- 모든 time step $t$에서, controller는 $x_{t}$와 $h_{t-1}$를 inputs로 하는 $h_{t}$에 대한 functional form을 찾아야 함.
- 가장 간단한 방법은 basic recurrent cell의 공식인 $h_{t} = tanh(W_{1} * x_{t} + W_{2}*h_{t-1})$을 갖는 것.
(더 복잡한 공식인 LSTM도 있음)
- 기본 RNN 및 LSTM 셀에 대한 계산은 $x_{t}$ 및 $h_{t-1}$을 입력으로 사용하고 $h_{t}$를 최종 출력으로 생성하는 단계 트리로 일반화 가능
- Controller RNN은 tree의 각 node에 두 개의 inputs을 병합하고 하나의 output을 생성하기 위해,
combination method(addition, elementwise multiplication, etc.)와 activation function(tanh, sigmoid, etc)의
label을 지정해야 한다.
- 그런 다음, 두개의 outputs이 트리의 다음 노드에 대한 inputs으로 제공.
- Controller RNN이 이러한 방법과 기능을 선택할 수 있도록, Controller RNN이 각 노드를 하나씩 방문하고 필요한 hyper-parameter에 label을 지정할 수 있도록 tree의 노드는 순서대로 인덱싱
- LSTM의 cell 구성에서 영감을 받아 memory state를 나타내기 위해 cell variables $c_{t-1}$ 및 $c_{t}$도 필요하다.
- 이러한 변수를 통합하려면 controller RNN이 이 두 변수를 연결한 tree의 node를 예측해야 함.
- 이러한 예측은 controller RNN의 마지막 두 blocks에서 수행할 수 있다.
아래의 그림을 봐보자

보면, Leaf node는 0과 1로 indexing되고, 내부 노드는 2로 indexing된다.
- Controller RNN은 먼저 3개의 block을 예측해야 하며, 각 block은 각 트리 index에 대한 combination method와 activation function을 지정
- 그 후, $c_{t-1}$ 및 $c_{t}$을 tree 내부의 임시 변수에 연결하는 방법을 지정하는 마지막 2개 block을 예측해야 한다.
- 특히, 이 예에서 controller RNN의 예측에 따라 다음 계산 단계가 발생한다.
Controller가 계산해야 할 것
- Tree index 0에 대해 $Add$ 와 $Tanh$를 예측 -> $a_{0} = tanh(W_{1} * x_{t} + W_{2} * h_{t-1})$을 계산해야 함
- Tree index 1에 대해 $ElemMult$와 $ReLU$를 예측 -> $a_{1} = ReLU((W_{3} * x_{t}) ⨀ (W_{4} * h_{t-1}))$을 계산해야 함
- "Cell Index"의 두 번째 요소에 대해 0을 예측하고, "Cell Inject"의 요소에 대해 Add & ReLU를 예측 -> $0 = ReLU(a_{0} + c_{t-1}$ 을 계산해야 함. (트리의 내부 노드에 대해 learnable parameter가 없음을 참고)
- Tree index 2에 대해 $ElemMult$와 $Sigmoid$를 예측 -> 이는 $a_{2} = sigmoid(a_0^\text{new} ⨀ a_{1}) $
- Tree의 index가 최대 2이므로 $h_{t}$는 $a_{2}$로 설정
- "Cell index"의 첫 번째 요소에 대해 1을 예측함. 이는 activation 전에 index 1에 있는 tree의 ouput으로 $c_{t}$를 설정해야 함을 의미 -> 즉 $c_t = (W_3 * x_t) ⨀ (W_4 * h_{t-1})$
위의 예에서 트리에는 두 개의 리프 노드가 있으므로 "base 2" architecture. 본 실험에서 cell이 expressive인지 확인하기 위해 base number 8을 사용.
Experiments
DATASETS
Image classification task: CIFAR-10
Language modeling task: Penn Treebank
- CIFAR-10에 대해서 좋은 convolutional architecture를 찾는 것이 목표(Penn Treebank의 경우 recurrent cell 찾는 것이 목표)
- 각 데이터셋에는 reward signal을 계산하기 위한 held-out validation dataset이 있다.
- Test set에 대해 보고된 performance은 held-out dataset에서 best result를 달성하는 네트워크에 대해 한 번만 계산
Learning Convolutional Architecture for CIFAR-10
DATASETS
- pre-process : whitening
- augmentation : upsample -> random 32x32 crop -> random horizontal flips
SEARCH SPACE
- Convolutional architectures
- ReLU
- batch normalization
- skip connections
- every convolutional layer - filter height [1, 3, 5, 7], filter width [1, 3, 5, 7], number of filters [24,36,48,64]
- stride - 1 or [1, 2, 3]
Training Details
- controller RNN : two-layer LSTM(35 hidden units on each layer)
- Adam optimizer, learning rate 0.0006
- Initialized uniformly between -0.08 ~ 0.08
- Distributed training : number of parameter server shards $S$ : 20
- controller replicas $K$ : 100
- number of child replicas $m$ : 8
- 800 networks being trained on 800 GPUs concurrently at any time.
Child Network
- Controller RNN이 architecture를 sampling하면 child model이 구성되고 50 epoch 동안 학습.
- Reward for controller update : 마지막 5개의 epoch의 maximum validation accuracy를 세제곱(cubed)한 것.
- Training set : 45,000 samples
- Validation set : 5,000 samples
- CIFAR-10 child model을 training하기 위한 setting은 DenseNet(Gao Huang, Zhuang Liu, and Kilian Q. Weinberger. Densely connected convolutional networks)과 동일
- Momentum Optimizer, learning rate 0.1, weight decay 1e-4, momentum 0.9, Nesterov Momentum
Controller를 training하는 동안, training이 진행됨에 따라 child network의 layer 수를 늘리는 schedule을 사용
CIFAR-10에서는 controller에 6개의 layer에서 시작하여, 1600개의 샘플마다 child network의 깊이를 2만큼 증가시키도록 controller에 요청.
Result
- 12,800개의 architecture를 controller가 학습, best validation accuracy를 달성하는 architecture를 찾는다.
- 그 후, small grid search 수행(learning rate, weight decay, batchnorm epsilon 및 learning rate를 감소시킬 epoch 찾기)
- 이 grid search의 best model은 convergence할 때까지 실행되고 그런 다음, 모델의 test accuracy를 측정
결과는 아래와 같음
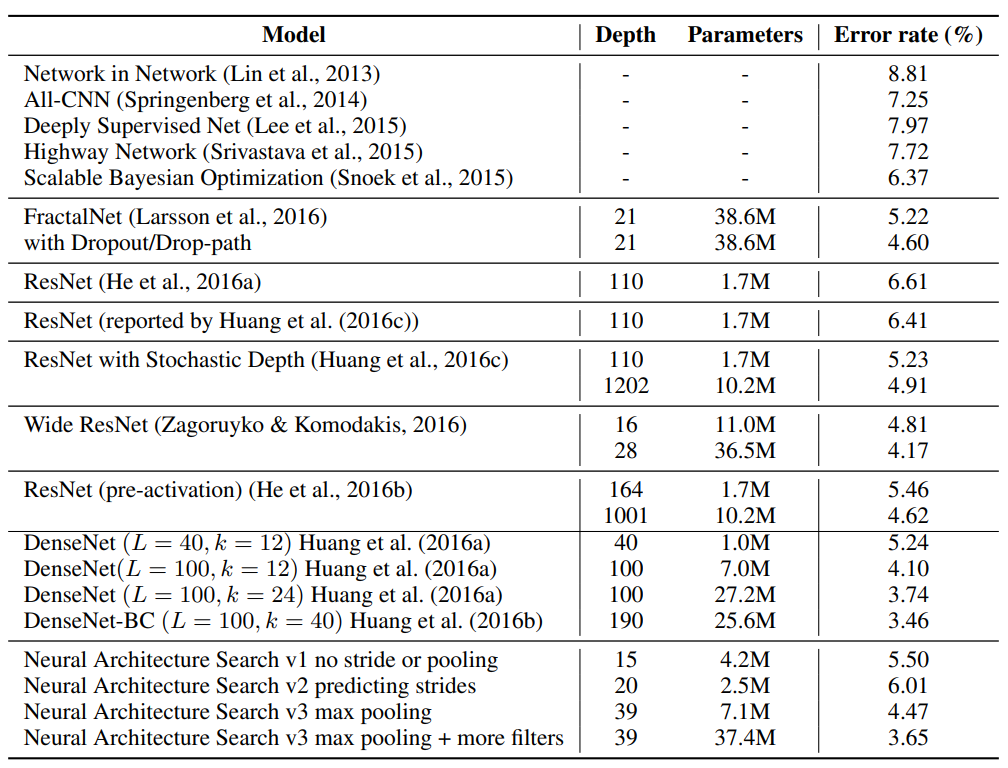
위 표에서 보면 NAS는 CIFAR-10에서, 가장 좋은 모델 중 일부만큼 성능이 뛰어난 몇 가지 promising한 architecture를 설계할 수 있다.
위 표에서 5.50%의 error rate를 달성하는 15-layer architecture의 그림은 아래와 같다.
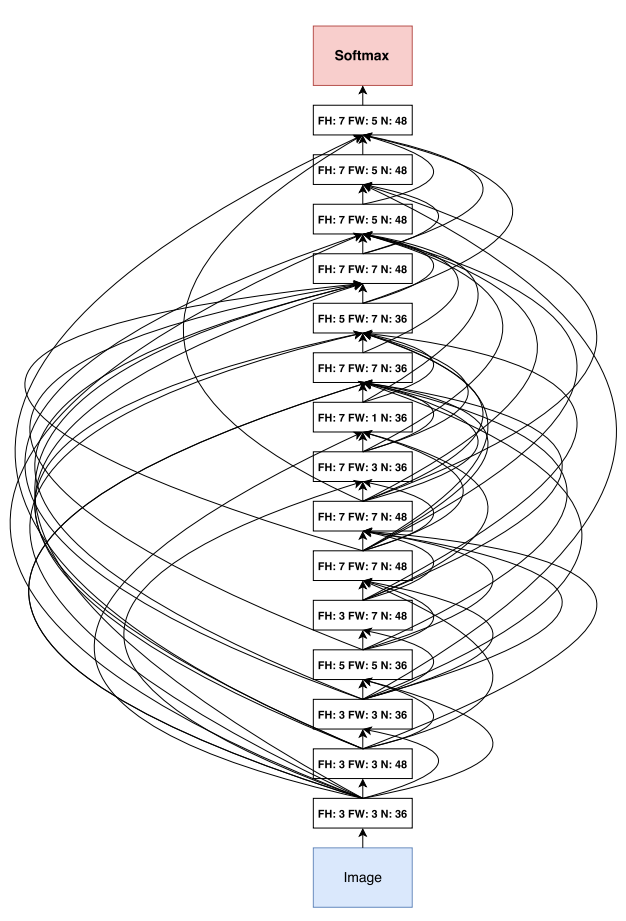
- 위 그림을 보면 직사각형 필터도 있고 뒤로 갈수록 더 큰 필터수를 선호한다는 것.
- 많은 skip connections들이 있음.
- 그러나 이 architecture는 교란(perturb)하면 performance가 악화된다는 점에서 local optimum이다.
- 모든 layer를 skip connections로 densely 연결하면 5.56%로 더 나빠진다.
- 모든 skip connections를 제거하면 7.97%로 떨어진다.